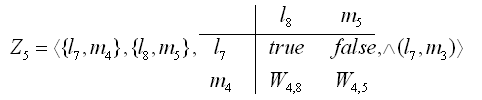Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Help:Formulas: Difference between revisions
start help page |
comparison |
||
| (5 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{help-pages/2}} | {{help-pages/2}} | ||
<div style="float:right; margin-left: .5em">__TOC__</div> | |||
Formulas on a wiki like Ifigenia can be represented in three ways, depending on the formula complexity and tools used: | Formulas on a wiki like Ifigenia can be represented in three ways, depending on the formula complexity and tools used: | ||
| Line 6: | Line 7: | ||
* TeX code - for formulas of any complexity - from very simple to extremely sophisticated | * TeX code - for formulas of any complexity - from very simple to extremely sophisticated | ||
Maybe, for the users of Ifigenia TeX-coded formulas may turn out to be the most natural ones. They allow relatively good integration with other TeX documents and they can be further saved as | Maybe, for the users of Ifigenia TeX-coded formulas may turn out to be the most natural ones. They allow relatively good integration with other TeX documents and they can be further saved as image files, for the sake of integration with MS Word documents. | ||
== Formulas in TeX == | == Formulas in TeX == | ||
In the wiki websites, TeX-formulas are distinguished from the rest of the text by enclosing them with the tags <code><math> </math></code>. A handy way is to click the Math button [[Image:Button_math.png]] and then write between the tags. | In the wiki websites, TeX-formulas are distinguished from the rest of the text by enclosing them with the tags <code><math> </math></code>. A handy way is to click the Math button [[Image:Button_math.png]] and then write between the tags. | ||
On Ifigenia, the TeX formulas are rendered using a [http://www.forkosh.com/mimetex.html public mimeTeX web service], so the process may be a bit slower, about 1 second per 1 <code><math></code>-call. | |||
Rendered TeX formulas can be stored on the hard disk as images in <code>.gif</code> format (default) or <code>.png</code> (optional). | |||
Here is a reference list for the various TeX commands in use. | |||
=== Functions, symbols, special characters === | |||
<!-- Eight symbols per line seems to be optimal--> | |||
{| class="wikitable" | |||
! colspan="2" |<h3>Accents/Diacritics</h3> | |||
|- | |||
|<code>\acute{a} \grave{a} \hat{a} \tilde{a} \breve{a}</code> | |||
|<math>\acute{a} \grave{a} \hat{a} \tilde{a} \breve{a}\,\!</math> | |||
|- | |||
|<code>\check{a} \bar{a} \ddot{a} \dot{a}</code> | |||
|<math>\check{a} \bar{a} \ddot{a} \dot{a}\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Standard functions</h3> | |||
|- | |||
|<code>\sin a \cos b \tan c</code> | |||
|<math>\sin a \cos b \tan c\,\!</math> | |||
|- | |||
|<code>\sec d \csc e \cot f</code> | |||
|<math>\sec d \csc e \cot f\,\!</math> | |||
|- | |||
|<code>\arcsin h \arccos i \arctan j</code> | |||
|<math>\arcsin h \arccos i \arctan j\,\!</math> | |||
|- | |||
|<code>\sinh k \cosh l \tanh m \coth n</code> | |||
|<math>\sinh k \cosh l \tanh m \coth n\,\!</math> | |||
|- | |||
|<code>\operatorname{sh}\,o\,\operatorname{ch}\,p\,\operatorname{th}\,q</code> | |||
|<math>\operatorname{sh}\,o\,\operatorname{ch}\,p\,\operatorname{th}\,q\,\!</math> | |||
|- | |||
|<code>\operatorname{arsinh}\,r\,\operatorname{arcosh}\,s\,\operatorname{artanh}\,t</code> | |||
|<math>\operatorname{arsinh}\,r\,\operatorname{arcosh}\,s\,\operatorname{artanh}\,t\,\!</math> | |||
|- | |||
|<code>\lim u \limsup v \liminf w \min x \max y</code> | |||
|<math>\lim u \limsup v \liminf w \min x \max y\,\!</math> | |||
|- | |||
|<code>\inf z \sup a \exp b \ln c \lg d \log e \log_{10} f \ker g</code> | |||
|<math>\inf z \sup a \exp b \ln c \lg d \log e \log_{10} f \ker g\,\!</math> | |||
|- | |||
|<code>\deg h \gcd i \Pr j \det k \hom l \arg m \dim n</code> | |||
|<math>\deg h \gcd i \Pr j \det k \hom l \arg m \dim n\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Modular arithmetic</h3> | |||
|- | |||
|<code>s_k \equiv 0 \pmod{m}</code> | |||
|<math>s_k \equiv 0 \pmod{m}\,\!</math> | |||
|- | |||
|<code>a\,\bmod\,b</code> | |||
|<math>a\,\bmod\,b\,\!</math> | |||
|- | |||
! colspan="2" | <h3>Derivatives</h3> | |||
|- | |||
|<code>\nabla \, \partial x \, dx \, \dot x \, \ddot y\, dy/dx\, \frac{dy}{dx}\, \frac{\partial^2 y}{\partial x_1\,\partial x_2}</code> | |||
|<math>\nabla \, \partial x \, dx \, \dot x \, \ddot y\, dy/dx\, \frac{dy}{dx}\, \frac{\partial^2 y}{\partial x_1\,\partial x_2}</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Sets</h3> | |||
|- | |||
|<code>\forall \exists \empty \emptyset \varnothing</code> | |||
|<math>\forall \exists \empty \emptyset \varnothing\,\!</math> | |||
|- | |||
|<code>\in \ni \not \in \notin \subset \subseteq \supset \supseteq</code> | |||
|<math>\in \ni \not \in \notin \subset \subseteq \supset \supseteq\,\!</math> | |||
|- | |||
|<code>\cap \bigcap \cup \bigcup \biguplus \setminus \smallsetminus</code> | |||
|<math>\cap \bigcap \cup \bigcup \biguplus \setminus \smallsetminus\,\!</math> | |||
|- | |||
|<code>\sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup</code> | |||
|<math>\sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Operators</h3> | |||
|- | |||
|<code>+ \oplus \bigoplus \pm \mp - </code> | |||
|<math>+ \oplus \bigoplus \pm \mp - \,\!</math> | |||
|- | |||
|<code>\times \otimes \bigotimes \cdot \circ \bullet \bigodot</code> | |||
|<math>\times \otimes \bigotimes \cdot \circ \bullet \bigodot\,\!</math> | |||
|- | |||
|<code>\star * / \div \frac{1}{2}</code> | |||
|<math>\star * / \div \frac{1}{2}\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Logic</h3> | |||
|- | |||
|<code>\land (or \and) \wedge \bigwedge \bar{q} \to p</code> | |||
|<math>\land \wedge \bigwedge \bar{q} \to p\,\!</math> | |||
|- | |||
|<code>\lor \vee \bigvee \lnot \neg q \And</code> | |||
|<math>\lor \vee \bigvee \lnot \neg q \And\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Root</h3> | |||
|- | |||
|<code>\sqrt{2} \sqrt[n]{x}</code> | |||
|<math>\sqrt{2} \sqrt[n]{x}\,\!</math> | |||
|- | |||
! colspan="2" | <h3>Relations</h3> | |||
|- | |||
|<code>\sim \approx \simeq \cong \dot= \overset{\underset{\mathrm{def}}{}}{=}</code> | |||
|<math>\sim \approx \simeq \cong \dot= \overset{\underset{\mathrm{def}}{}}{=}\,\!</math> | |||
|- | |||
|<code>\le < \ll \gg \ge > \equiv \not\equiv \ne \mbox{or} \neq \propto</code> | |||
|<math>\le < \ll \gg \ge > \equiv \not\equiv \ne \mbox{or} \neq \propto\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Geometric</h3> | |||
|- | |||
|<code><nowiki>\Diamond \Box \triangle \angle \perp \mid \nmid \| 45^\circ</nowiki></code> | |||
|<math>\Diamond \, \Box \, \triangle \, \angle \perp \, \mid \; \nmid \, \| 45^\circ\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Arrows</h3> | |||
|- | |||
|<code>\leftarrow (or \gets) \rightarrow (or \to) \nleftarrow \nrightarrow \leftrightarrow \nleftrightarrow \longleftarrow \longrightarrow \longleftrightarrow</code> | |||
|<math>\leftarrow \rightarrow \nleftarrow \not\to \leftrightarrow \nleftrightarrow \longleftarrow \longrightarrow \longleftrightarrow \,\!</math> | |||
|- | |||
|<code>\Leftarrow \Rightarrow \nLeftarrow \nRightarrow \Leftrightarrow \nLeftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow (or \iff)</code> | |||
|<math>\Leftarrow \Rightarrow \nLeftarrow \nRightarrow \Leftrightarrow \nLeftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow \,\!</math> | |||
|- | |||
|<code>\uparrow \downarrow \updownarrow \Uparrow \Downarrow \Updownarrow \nearrow \searrow \swarrow \nwarrow</code> | |||
|<math>\uparrow \downarrow \updownarrow \Uparrow \Downarrow \Updownarrow \nearrow \searrow \swarrow \nwarrow \,\!</math> | |||
|- | |||
|<code>\rightharpoonup \rightharpoondown \leftharpoonup \leftharpoondown \upharpoonleft \upharpoonright \downharpoonleft \downharpoonright \rightleftharpoons \leftrightharpoons</code> | |||
|<math>\rightharpoonup \rightharpoondown \leftharpoonup \leftharpoondown \upharpoonleft \upharpoonright \downharpoonleft \downharpoonright \rightleftharpoons \leftrightharpoons \,\!</math> | |||
|- | |||
|<code>\curvearrowleft \circlearrowleft \Lsh \upuparrows \rightrightarrows \rightleftarrows \Rrightarrow \rightarrowtail \looparrowright</code> | |||
|<math>\curvearrowleft \circlearrowleft \Lsh \upuparrows \rightrightarrows \rightleftarrows \Rrightarrow \rightarrowtail \looparrowright \,\!</math> | |||
|- | |||
|<code>\curvearrowright \circlearrowright \Rsh \downdownarrows \leftleftarrows \leftrightarrows \Lleftarrow \leftarrowtail \looparrowleft</code> | |||
|<math>\curvearrowright \circlearrowright \Rsh \downdownarrows \leftleftarrows \leftrightarrows \Lleftarrow \leftarrowtail \looparrowleft \,\!</math> | |||
|- | |||
|<code>\mapsto \longmapsto \hookrightarrow \hookleftarrow \multimap \leftrightsquigarrow \rightsquigarrow </code> | |||
|<math>\mapsto \longmapsto \hookrightarrow \hookleftarrow \multimap \leftrightsquigarrow \rightsquigarrow \,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Special</h3> | |||
|- | |||
|<code>\And \eth \S \P \% \dagger \ddagger \ldots \cdots</code> | |||
|<math>\And \eth \S \P \% \dagger \ddagger \ldots \cdots\,\!</math> | |||
|- | |||
|<code>\smile \frown \wr \triangleleft \triangleright \infty \bot \top</code> | |||
|<math>\smile \frown \wr \triangleleft \triangleright \infty \bot \top\,\!</math> | |||
|- | |||
|<code>\vdash \vDash \Vdash \models \lVert \rVert \imath \hbar</code> | |||
|<math>\vdash \vDash \Vdash \models \lVert \rVert \imath \hbar\,\!</math> | |||
|- | |||
|<code>\ell \mho \Finv \Re \Im \wp \complement</code> | |||
|<math>\ell \mho \Finv \Re \Im \wp \complement\,\!</math> | |||
|- | |||
|<code>\diamondsuit \heartsuit \clubsuit \spadesuit \Game \flat \natural \sharp</code> | |||
|<math>\diamondsuit \heartsuit \clubsuit \spadesuit \Game \flat \natural \sharp\,\!</math> | |||
|- | |||
! colspan="2" | | |||
<h3>Unsorted (new stuff)</h3> | |||
|- | |||
|<code> \vartriangle \triangledown \lozenge \circledS \measuredangle \nexists \Bbbk \backprime \blacktriangle \blacktriangledown</code> | |||
|<math> \vartriangle \triangledown \lozenge \circledS \measuredangle \nexists \Bbbk \backprime \blacktriangle \blacktriangledown</math> | |||
|- | |||
|<code> \blacksquare \blacklozenge \bigstar \sphericalangle \diagup \diagdown \dotplus \Cap \Cup \barwedge</code> | |||
|<math> \blacksquare \blacklozenge \bigstar \sphericalangle \diagup \diagdown \dotplus \Cap \Cup \barwedge</math> | |||
|- | |||
|<code> \veebar \doublebarwedge \boxminus \boxtimes \boxdot \boxplus \divideontimes \ltimes \rtimes \leftthreetimes</code> | |||
|<math> \veebar \doublebarwedge \boxminus \boxtimes \boxdot \boxplus \divideontimes \ltimes \rtimes \leftthreetimes</math> | |||
|- | |||
|<code> \rightthreetimes \curlywedge \curlyvee \circleddash \circledast \circledcirc \centerdot \intercal \leqq \leqslant</code> | |||
|<math> \rightthreetimes \curlywedge \curlyvee \circleddash \circledast \circledcirc \centerdot \intercal \leqq \leqslant</math> | |||
|- | |||
|<code> \eqslantless \lessapprox \approxeq \lessdot \lll \lessgtr \lesseqgtr \lesseqqgtr \doteqdot \risingdotseq</code> | |||
|<math> \eqslantless \lessapprox \approxeq \lessdot \lll \lessgtr \lesseqgtr \lesseqqgtr \doteqdot \risingdotseq</math> | |||
|- | |||
|<code> \fallingdotseq \backsim \backsimeq \subseteqq \Subset \preccurlyeq \curlyeqprec \precsim \precapprox \vartriangleleft</code> | |||
|<math> \fallingdotseq \backsim \backsimeq \subseteqq \Subset \preccurlyeq \curlyeqprec \precsim \precapprox \vartriangleleft</math> | |||
|- | |||
|<code> \Vvdash \bumpeq \Bumpeq \geqq \geqslant \eqslantgtr \gtrsim \gtrapprox \eqsim \gtrdot</code> | |||
|<math> \Vvdash \bumpeq \Bumpeq \geqq \geqslant \eqslantgtr \gtrsim \gtrapprox \eqsim \gtrdot</math> | |||
|- | |||
|<code> \ggg \gtrless \gtreqless \gtreqqless \eqcirc \circeq \triangleq \thicksim \thickapprox \supseteqq</code> | |||
|<math> \ggg \gtrless \gtreqless \gtreqqless \eqcirc \circeq \triangleq \thicksim \thickapprox \supseteqq</math> | |||
|- | |||
|<code> \Supset \succcurlyeq \curlyeqsucc \succsim \succapprox \vartriangleright \shortmid \shortparallel \between \pitchfork</code> | |||
|<math> \Supset \succcurlyeq \curlyeqsucc \succsim \succapprox \vartriangleright \shortmid \shortparallel \between \pitchfork</math> | |||
|- | |||
|<code> \varpropto \blacktriangleleft \therefore \backepsilon \blacktriangleright \because \nleqslant \nleqq \lneq \lneqq</code> | |||
|<math> \varpropto \blacktriangleleft \therefore \backepsilon \blacktriangleright \because \nleqslant \nleqq \lneq \lneqq</math> | |||
|- | |||
|<code> \lvertneqq \lnsim \lnapprox \nprec \npreceq \precneqq \precnsim \precnapprox \nsim \nshortmid</code> | |||
|<math> \lvertneqq \lnsim \lnapprox \nprec \npreceq \precneqq \precnsim \precnapprox \nsim \nshortmid</math> | |||
|- | |||
|<code> \nvdash \nVdash \ntriangleleft \ntrianglelefteq \nsubseteq \nsubseteqq \varsubsetneq \subsetneqq \varsubsetneqq \ngtr</code> | |||
|<math> \nvdash \nVdash \ntriangleleft \ntrianglelefteq \nsubseteq \nsubseteqq \varsubsetneq \subsetneqq \varsubsetneqq \ngtr</math> | |||
|- | |||
|<code>\subsetneq</code> | |||
|<math>\subsetneq</math> | |||
|- | |||
|<code> \ngeqslant \ngeqq \gneq \gneqq \gvertneqq \gnsim \gnapprox \nsucc \nsucceq \succneqq</code> | |||
|<math> \ngeqslant \ngeqq \gneq \gneqq \gvertneqq \gnsim \gnapprox \nsucc \nsucceq \succneqq</math> | |||
|- | |||
|<code> \succnsim \succnapprox \ncong \nshortparallel \nparallel \nvDash \nVDash \ntriangleright \ntrianglerighteq \nsupseteq</code> | |||
|<math> \succnsim \succnapprox \ncong \nshortparallel \nparallel \nvDash \nVDash \ntriangleright \ntrianglerighteq \nsupseteq</math> | |||
|- | |||
|<code> \nsupseteqq \varsupsetneq \supsetneqq \varsupsetneqq</code> | |||
|<math> \nsupseteqq \varsupsetneq \supsetneqq \varsupsetneqq</math> | |||
|- | |||
|<code>\jmath \surd \ast \uplus \diamond \bigtriangleup \bigtriangledown \ominus</code> | |||
|<math>\jmath \surd \ast \uplus \diamond \bigtriangleup \bigtriangledown \ominus\,\!</math> | |||
|- | |||
|<code>\oslash \odot \bigcirc \amalg \prec \succ \preceq \succeq</code> | |||
|<math>\oslash \odot \bigcirc \amalg \prec \succ \preceq \succeq\,\!</math> | |||
|- | |||
|<code>\dashv \asymp \doteq \parallel</code> | |||
|<math>\dashv \asymp \doteq \parallel\,\!</math> | |||
|- | |||
|<code>\ulcorner \urcorner \llcorner \lrcorner</code> | |||
|<math>\ulcorner \urcorner \llcorner \lrcorner</math> | |||
|} | |||
=== Subscripts, superscripts, integrals === | |||
{| border="2" cellpadding="4" cellspacing="0" style="margin: 1em 1em 1em 0; background: #f9f9f9; border: 1px #aaa solid; border-collapse: collapse;" | |||
!rowspan="2"|Feature!!rowspan="2"|Syntax!!colspan="2"|How it looks rendered | |||
|- | |||
!HTML!!PNG | |||
|- | |||
|- | |||
|Superscript||<code>a^2</code>||<math>a^2</math>||<math>a^2 \,\!</math> | |||
|- | |||
|Subscript||<code>a_2</code>||<math>a_2</math>||<math>a_2 \,\!</math> | |||
|- | |||
|rowspan=2|Grouping||<code>a^{2+2}</code>||<math>a^{2+2}</math>||<math>a^{2+2}\,\!</math> | |||
|- | |||
|<code>a_{i,j}</code>||<math>a_{i,j}</math>||<math>a_{i,j}\,\!</math> | |||
|- | |||
|Combining sub & super||<code>x_2^3</code>||colspan=2|<math>x_2^3</math> | |||
|- | |||
|Super super||<code>10^{10^{ \,\!{8} }</code>||colspan=2|<math>10^{10^{ \,\! 8 } }</math> | |||
|- | |||
|Super super||<code>10^{10^{ \overset{8}{} }}</code>||colspan=2|<math>10^{10^{ \overset{8}{} }}</math> | |||
|- | |||
|Super super (wrong in HTML in some browsers)||<code>10^{10^8}</code> ||colspan=2|<math>10^{10^8}</math> | |||
|- | |||
|rowspan="2"|Preceding and/or Additional sub & super||<code>\sideset{_1^2}{_3^4}\prod_a^b</code>||colspan=2|<math>\sideset{_1^2}{_3^4}\prod_a^b</math> | |||
|- | |||
|<code>{}_1^2\!\Omega_3^4</code>||colspan=2|<math>{}_1^2\!\Omega_3^4</math> | |||
|- | |||
|rowspan="4"|Stacking | |||
|<code>\overset{\alpha}{\omega}</code>||colspan="2"|<math>\overset{\alpha}{\omega}</math> | |||
|- | |||
|<code>\underset{\alpha}{\omega}</code>||colspan="2"|<math>\underset{\alpha}{\omega}</math> | |||
|- | |||
|<code>\overset{\alpha}{\underset{\gamma}{\omega}}</code>||colspan="2"|<math>\overset{\alpha}{\underset{\gamma}{\omega}}</math> | |||
|- | |||
|<code>\stackrel{\alpha}{\omega}</code>||colspan="2"|<math>\stackrel{\alpha}{\omega}</math> | |||
|- | |||
|Derivative (forced PNG)||<code>x', y<nowiki>''</nowiki>, f', f<nowiki>''</nowiki>\!</code>|| ||<math>x', y'', f', f''\!</math> | |||
|- | |||
|Derivative (f in italics may overlap primes in HTML)||<code>x', y<nowiki>''</nowiki>, f', f<nowiki>''</nowiki></code>||<math>x', y'', f', f''</math>||<math>x', y'', f', f''\!</math> | |||
|- | |||
|Derivative (wrong in HTML)||<code>x^\prime, y^{\prime\prime}</code>||<math>x^\prime, y^{\prime\prime}</math>||<math>x^\prime, y^{\prime\prime}\,\!</math> | |||
|- | |||
|Derivative (wrong in PNG)||<code>x\prime, y\prime\prime</code>||<math>x\prime, y\prime\prime</math>||<math>x\prime, y\prime\prime\,\!</math> | |||
|- | |||
|Derivative dots||<code>\dot{x}, \ddot{x}</code>||colspan=2|<math>\dot{x}, \ddot{x}</math> | |||
|- | |||
|rowspan="3"|Underlines, overlines, vectors||<code>\hat a \ \bar b \ \vec c</code>||colspan=2|<math>\hat a \ \bar b \ \vec c</math> | |||
|- | |||
|<code>\overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f}</code>||colspan=2|<math>\overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f}</math> | |||
|- | |||
|<code>\overline{g h i} \ \underline{j k l}</code>||colspan=2|<math>\overline{g h i} \ \underline{j k l}</math> | |||
|- | |||
|Arrows||<code> A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C</code>||colspan=2|<math> A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C</math> | |||
|- | |||
|Overbraces||<code>\overbrace{ 1+2+\cdots+100 }^{5050}</code>||colspan=2|<math>\overbrace{ 1+2+\cdots+100 }^{5050}</math> | |||
|- | |||
|Underbraces||<code>\underbrace{ a+b+\cdots+z }_{26}</code>||colspan=2|<math>\underbrace{ a+b+\cdots+z }_{26}</math> | |||
|- | |||
|Sum||<code>\sum_{k=1}^N k^2</code>||colspan=2|<math>\sum_{k=1}^N k^2</math> | |||
|- | |||
|Sum (force <code>\textstyle</code>)||<code>\textstyle \sum_{k=1}^N k^2 </code>||colspan=2|<math>\textstyle \sum_{k=1}^N k^2</math> | |||
|- | |||
|Product||<code>\prod_{i=1}^N x_i</code>||colspan=2|<math>\prod_{i=1}^N x_i</math> | |||
|- | |||
|Product (force <code>\textstyle</code>)||<code>\textstyle \prod_{i=1}^N x_i</code>||colspan=2|<math>\textstyle \prod_{i=1}^N x_i</math> | |||
|- | |||
|Coproduct||<code>\coprod_{i=1}^N x_i</code>||colspan=2|<math>\coprod_{i=1}^N x_i</math> | |||
|- | |||
|Coproduct (force <code>\textstyle</code>)||<code>\textstyle \coprod_{i=1}^N x_i</code>||colspan=2|<math>\textstyle \coprod_{i=1}^N x_i</math> | |||
|- | |||
|Limit||<code>\lim_{n \to \infty}x_n</code>||colspan=2|<math>\lim_{n \to \infty}x_n</math> | |||
|- | |||
|Limit (force <code>\textstyle</code>)||<code>\textstyle \lim_{n \to \infty}x_n</code>||colspan=2|<math>\textstyle \lim_{n \to \infty}x_n</math> | |||
|- | |||
|Integral||<code>\int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx</code>||colspan=2|<math>\int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx</math> | |||
|- | |||
|Integral (alternate limits style)||<code>\int_{1}^{3}\frac{e^3/x}{x^2}\, dx</code>||colspan=2|<math>\int_{1}^{3}\frac{e^3/x}{x^2}\, dx</math> | |||
|- | |||
|Integral (force <code>\textstyle</code>)||<code>\textstyle \int\limits_{-N}^{N} e^x\, dx</code>||colspan=2|<math>\textstyle \int\limits_{-N}^{N} e^x\, dx</math> | |||
|- | |||
|Integral (force <code>\textstyle</code>, alternate limits style)||<code>\textstyle \int_{-N}^{N} e^x\, dx</code>||colspan=2|<math>\textstyle \int_{-N}^{N} e^x\, dx</math> | |||
|- | |||
|Double integral||<code>\iint\limits_D \, dx\,dy</code>||colspan=2|<math>\iint\limits_D \, dx\,dy</math> | |||
|- | |||
|Triple integral||<code>\iiint\limits_E \, dx\,dy\,dz</code>||colspan=2|<math>\iiint\limits_E \, dx\,dy\,dz</math> | |||
|- | |||
|Quadruple integral||<code>\iiiint\limits_F \, dx\,dy\,dz\,dt</code>||colspan=2|<math>\iiiint\limits_F \, dx\,dy\,dz\,dt</math> | |||
|- | |||
|Line or path integral||<code>\int_C x^3\, dx + 4y^2\, dy</code>||colspan=2|<math>\int_C x^3\, dx + 4y^2\, dy</math> | |||
|- | |||
|Closed line or path integral||<code>\oint_C x^3\, dx + 4y^2\, dy</code>||colspan=2|<math>\oint_C x^3\, dx + 4y^2\, dy</math> | |||
|- | |||
|Intersections||<code>\bigcap_1^n p</code>||colspan=2|<math>\bigcap_1^n p</math> | |||
|- | |||
|Unions||<code>\bigcup_1^k p</code>||colspan=2|<math>\bigcup_1^k p</math> | |||
|} | |||
=== Alphabets and typefaces === | |||
{| class="wikitable" | |||
! colspan="2" | Greek alphabet | |||
|- | |||
|<code><nowiki>\Alpha \Beta \Gamma \Delta \Epsilon \Zeta</nowiki></code> | |||
|<math>\Alpha \Beta \Gamma \Delta \Epsilon \Zeta \,\!</math> | |||
|- | |||
|<code><nowiki>\Eta \Theta \Iota \Kappa \Lambda \Mu</nowiki></code> | |||
|<math>\Eta \Theta \Iota \Kappa \Lambda \Mu \,\!</math> | |||
|- | |||
|<code><nowiki>\Nu \Xi \Pi \Rho \Sigma \Tau</nowiki></code> | |||
|<math>\Nu \Xi \Pi \Rho \Sigma \Tau\,\!</math> | |||
|- | |||
|<code><nowiki>\Upsilon \Phi \Chi \Psi \Omega</nowiki></code> | |||
|<math>\Upsilon \Phi \Chi \Psi \Omega \,\!</math> | |||
|- | |||
|<code><nowiki>\alpha \beta \gamma \delta \epsilon \zeta</nowiki></code> | |||
|<math>\alpha \beta \gamma \delta \epsilon \zeta \,\!</math> | |||
|- | |||
|<code><nowiki>\eta \theta \iota \kappa \lambda \mu</nowiki></code> | |||
|<math>\eta \theta \iota \kappa \lambda \mu \,\!</math> | |||
|- | |||
|<code><nowiki>\nu \xi \pi \rho \sigma \tau</nowiki></code> | |||
|<math>\nu \xi \pi \rho \sigma \tau \,\!</math> | |||
|- | |||
|<code><nowiki>\upsilon \phi \chi \psi \omega</nowiki></code> | |||
|<math>\upsilon \phi \chi \psi \omega \,\!</math> | |||
|- | |||
|<code><nowiki>\varepsilon \digamma \vartheta \varkappa</nowiki></code> | |||
|<math>\varepsilon \digamma \vartheta \varkappa \,\!</math> | |||
|- | |||
|<code><nowiki>\varpi \varrho \varsigma \varphi</nowiki></code> | |||
|<math>\varpi \varrho \varsigma \varphi\,\!</math> | |||
|- | |||
! colspan="2" | Blackboard Bold/Scripts | |||
|- | |||
|<code><nowiki>\mathbb{A} \mathbb{B} \mathbb{C} \mathbb{D} \mathbb{E} \mathbb{F} \mathbb{G}</nowiki></code> | |||
|<math>\mathbb{A} \mathbb{B} \mathbb{C} \mathbb{D} \mathbb{E} \mathbb{F} \mathbb{G} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbb{H} \mathbb{I} \mathbb{J} \mathbb{K} \mathbb{L} \mathbb{M}</nowiki></code> | |||
|<math>\mathbb{H} \mathbb{I} \mathbb{J} \mathbb{K} \mathbb{L} \mathbb{M} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbb{N} \mathbb{O} \mathbb{P} \mathbb{Q} \mathbb{R} \mathbb{S} \mathbb{T}</nowiki></code> | |||
|<math>\mathbb{N} \mathbb{O} \mathbb{P} \mathbb{Q} \mathbb{R} \mathbb{S} \mathbb{T} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbb{U} \mathbb{V} \mathbb{W} \mathbb{X} \mathbb{Y} \mathbb{Z}</nowiki></code> | |||
|<math>\mathbb{U} \mathbb{V} \mathbb{W} \mathbb{X} \mathbb{Y} \mathbb{Z}\,\!</math> | |||
|- | |||
! colspan="2" | boldface (vectors) | |||
|- | |||
|<code><nowiki>\mathbf{A} \mathbf{B} \mathbf{C} \mathbf{D} \mathbf{E} \mathbf{F} \mathbf{G}</nowiki></code> | |||
|<math>\mathbf{A} \mathbf{B} \mathbf{C} \mathbf{D} \mathbf{E} \mathbf{F} \mathbf{G} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{H} \mathbf{I} \mathbf{J} \mathbf{K} \mathbf{L} \mathbf{M}</nowiki></code> | |||
|<math>\mathbf{H} \mathbf{I} \mathbf{J} \mathbf{K} \mathbf{L} \mathbf{M} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{N} \mathbf{O} \mathbf{P} \mathbf{Q} \mathbf{R} \mathbf{S} \mathbf{T}</nowiki></code> | |||
|<math>\mathbf{N} \mathbf{O} \mathbf{P} \mathbf{Q} \mathbf{R} \mathbf{S} \mathbf{T} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{U} \mathbf{V} \mathbf{W} \mathbf{X} \mathbf{Y} \mathbf{Z}</nowiki></code> | |||
|<math>\mathbf{U} \mathbf{V} \mathbf{W} \mathbf{X} \mathbf{Y} \mathbf{Z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{a} \mathbf{b} \mathbf{c} \mathbf{d} \mathbf{e} \mathbf{f} \mathbf{g}</nowiki></code> | |||
|<math>\mathbf{a} \mathbf{b} \mathbf{c} \mathbf{d} \mathbf{e} \mathbf{f} \mathbf{g} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{h} \mathbf{i} \mathbf{j} \mathbf{k} \mathbf{l} \mathbf{m}</nowiki></code> | |||
|<math>\mathbf{h} \mathbf{i} \mathbf{j} \mathbf{k} \mathbf{l} \mathbf{m} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{n} \mathbf{o} \mathbf{p} \mathbf{q} \mathbf{r} \mathbf{s} \mathbf{t}</nowiki></code> | |||
|<math>\mathbf{n} \mathbf{o} \mathbf{p} \mathbf{q} \mathbf{r} \mathbf{s} \mathbf{t} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{u} \mathbf{v} \mathbf{w} \mathbf{x} \mathbf{y} \mathbf{z}</nowiki></code> | |||
|<math>\mathbf{u} \mathbf{v} \mathbf{w} \mathbf{x} \mathbf{y} \mathbf{z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{0} \mathbf{1} \mathbf{2} \mathbf{3} \mathbf{4}</nowiki></code> | |||
|<math>\mathbf{0} \mathbf{1} \mathbf{2} \mathbf{3} \mathbf{4} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathbf{5} \mathbf{6} \mathbf{7} \mathbf{8} \mathbf{9}</nowiki></code> | |||
|<math>\mathbf{5} \mathbf{6} \mathbf{7} \mathbf{8} \mathbf{9}\,\!</math> | |||
|- | |||
! colspan="2" | Boldface (greek) | |||
|- | |||
|<code><nowiki>\boldsymbol{\Alpha} \boldsymbol{\Beta} \boldsymbol{\Gamma} \boldsymbol{\Delta} \boldsymbol{\Epsilon} \boldsymbol{\Zeta}</nowiki></code> | |||
|<math>\boldsymbol{\Alpha} \boldsymbol{\Beta} \boldsymbol{\Gamma} \boldsymbol{\Delta} \boldsymbol{\Epsilon} \boldsymbol{\Zeta} \,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\Eta} \boldsymbol{\Theta} \boldsymbol{\Iota} \boldsymbol{\Kappa} \boldsymbol{\Lambda} \boldsymbol{\Mu}</nowiki></code> | |||
|<math>\boldsymbol{\Eta} \boldsymbol{\Theta} \boldsymbol{\Iota} \boldsymbol{\Kappa} \boldsymbol{\Lambda} \boldsymbol{\Mu}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\Nu} \boldsymbol{\Xi} \boldsymbol{\Pi} \boldsymbol{\Rho} \boldsymbol{\Sigma} \boldsymbol{\Tau}</nowiki></code> | |||
|<math>\boldsymbol{\Nu} \boldsymbol{\Xi} \boldsymbol{\Pi} \boldsymbol{\Rho} \boldsymbol{\Sigma} \boldsymbol{\Tau}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\Upsilon} \boldsymbol{\Phi} \boldsymbol{\Chi} \boldsymbol{\Psi} \boldsymbol{\Omega}</nowiki></code> | |||
|<math>\boldsymbol{\Upsilon} \boldsymbol{\Phi} \boldsymbol{\Chi} \boldsymbol{\Psi} \boldsymbol{\Omega}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\alpha} \boldsymbol{\beta} \boldsymbol{\gamma} \boldsymbol{\delta} \boldsymbol{\epsilon} \boldsymbol{\zeta}</nowiki></code> | |||
|<math>\boldsymbol{\alpha} \boldsymbol{\beta} \boldsymbol{\gamma} \boldsymbol{\delta} \boldsymbol{\epsilon} \boldsymbol{\zeta}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\eta} \boldsymbol{\theta} \boldsymbol{\iota} \boldsymbol{\kappa} \boldsymbol{\lambda} \boldsymbol{\mu}</nowiki></code> | |||
|<math>\boldsymbol{\eta} \boldsymbol{\theta} \boldsymbol{\iota} \boldsymbol{\kappa} \boldsymbol{\lambda} \boldsymbol{\mu}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\nu} \boldsymbol{\xi} \boldsymbol{\pi} \boldsymbol{\rho} \boldsymbol{\sigma} \boldsymbol{\tau}</nowiki></code> | |||
|<math>\boldsymbol{\nu} \boldsymbol{\xi} \boldsymbol{\pi} \boldsymbol{\rho} \boldsymbol{\sigma} \boldsymbol{\tau}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\upsilon} \boldsymbol{\phi} \boldsymbol{\chi} \boldsymbol{\psi} \boldsymbol{\omega}</nowiki></code> | |||
|<math>\boldsymbol{\upsilon} \boldsymbol{\phi} \boldsymbol{\chi} \boldsymbol{\psi} \boldsymbol{\omega}\,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\varepsilon} \boldsymbol{\digamma} \boldsymbol{\vartheta} \boldsymbol{\varkappa}</nowiki></code> | |||
|<math>\boldsymbol{\varepsilon} \boldsymbol{\digamma} \boldsymbol{\vartheta} \boldsymbol{\varkappa} \,\!</math> | |||
|- | |||
|<code><nowiki>\boldsymbol{\varpi} \boldsymbol{\varrho} \boldsymbol{\varsigma} \boldsymbol{\varphi}</nowiki></code> | |||
|<math>\boldsymbol{\varpi} \boldsymbol{\varrho} \boldsymbol{\varsigma} \boldsymbol{\varphi}\,\!</math> | |||
|- | |||
! colspan="2" | Italics | |||
|- | |||
|<code><nowiki>\mathit{A} \mathit{B} \mathit{C} \mathit{D} \mathit{E} \mathit{F} \mathit{G}</nowiki></code> | |||
|<math>\mathit{A} \mathit{B} \mathit{C} \mathit{D} \mathit{E} \mathit{F} \mathit{G} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{H} \mathit{I} \mathit{J} \mathit{K} \mathit{L} \mathit{M}</nowiki></code> | |||
|<math>\mathit{H} \mathit{I} \mathit{J} \mathit{K} \mathit{L} \mathit{M} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{N} \mathit{O} \mathit{P} \mathit{Q} \mathit{R} \mathit{S} \mathit{T}</nowiki></code> | |||
|<math>\mathit{N} \mathit{O} \mathit{P} \mathit{Q} \mathit{R} \mathit{S} \mathit{T} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{U} \mathit{V} \mathit{W} \mathit{X} \mathit{Y} \mathit{Z}</nowiki></code> | |||
|<math>\mathit{U} \mathit{V} \mathit{W} \mathit{X} \mathit{Y} \mathit{Z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{a} \mathit{b} \mathit{c} \mathit{d} \mathit{e} \mathit{f} \mathit{g}</nowiki></code> | |||
|<math>\mathit{a} \mathit{b} \mathit{c} \mathit{d} \mathit{e} \mathit{f} \mathit{g} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{h} \mathit{i} \mathit{j} \mathit{k} \mathit{l} \mathit{m}</nowiki></code> | |||
|<math>\mathit{h} \mathit{i} \mathit{j} \mathit{k} \mathit{l} \mathit{m} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{n} \mathit{o} \mathit{p} \mathit{q} \mathit{r} \mathit{s} \mathit{t}</nowiki></code> | |||
|<math>\mathit{n} \mathit{o} \mathit{p} \mathit{q} \mathit{r} \mathit{s} \mathit{t} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{u} \mathit{v} \mathit{w} \mathit{x} \mathit{y} \mathit{z}</nowiki></code> | |||
|<math>\mathit{u} \mathit{v} \mathit{w} \mathit{x} \mathit{y} \mathit{z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{0} \mathit{1} \mathit{2} \mathit{3} \mathit{4}</nowiki></code> | |||
|<math>\mathit{0} \mathit{1} \mathit{2} \mathit{3} \mathit{4} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathit{5} \mathit{6} \mathit{7} \mathit{8} \mathit{9}</nowiki></code> | |||
|<math>\mathit{5} \mathit{6} \mathit{7} \mathit{8} \mathit{9}\,\!</math> | |||
|- | |||
! colspan="2" | Roman typeface | |||
|- | |||
|<code><nowiki>\mathrm{A} \mathrm{B} \mathrm{C} \mathrm{D} \mathrm{E} \mathrm{F} \mathrm{G}</nowiki></code> | |||
|<math>\mathrm{A} \mathrm{B} \mathrm{C} \mathrm{D} \mathrm{E} \mathrm{F} \mathrm{G} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{H} \mathrm{I} \mathrm{J} \mathrm{K} \mathrm{L} \mathrm{M}</nowiki></code> | |||
|<math>\mathrm{H} \mathrm{I} \mathrm{J} \mathrm{K} \mathrm{L} \mathrm{M} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{N} \mathrm{O} \mathrm{P} \mathrm{Q} \mathrm{R} \mathrm{S} \mathrm{T}</nowiki></code> | |||
|<math>\mathrm{N} \mathrm{O} \mathrm{P} \mathrm{Q} \mathrm{R} \mathrm{S} \mathrm{T} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{U} \mathrm{V} \mathrm{W} \mathrm{X} \mathrm{Y} \mathrm{Z}</nowiki></code> | |||
|<math>\mathrm{U} \mathrm{V} \mathrm{W} \mathrm{X} \mathrm{Y} \mathrm{Z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{a} \mathrm{b} \mathrm{c} \mathrm{d} \mathrm{e} \mathrm{f} \mathrm{g}</nowiki></code> | |||
|<math>\mathrm{a} \mathrm{b} \mathrm{c} \mathrm{d} \mathrm{e} \mathrm{f} \mathrm{g}\,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{h} \mathrm{i} \mathrm{j} \mathrm{k} \mathrm{l} \mathrm{m}</nowiki></code> | |||
|<math>\mathrm{h} \mathrm{i} \mathrm{j} \mathrm{k} \mathrm{l} \mathrm{m} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{n} \mathrm{o} \mathrm{p} \mathrm{q} \mathrm{r} \mathrm{s} \mathrm{t}</nowiki></code> | |||
|<math>\mathrm{n} \mathrm{o} \mathrm{p} \mathrm{q} \mathrm{r} \mathrm{s} \mathrm{t} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{u} \mathrm{v} \mathrm{w} \mathrm{x} \mathrm{y} \mathrm{z}</nowiki></code> | |||
|<math>\mathrm{u} \mathrm{v} \mathrm{w} \mathrm{x} \mathrm{y} \mathrm{z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{0} \mathrm{1} \mathrm{2} \mathrm{3} \mathrm{4}</nowiki></code> | |||
|<math>\mathrm{0} \mathrm{1} \mathrm{2} \mathrm{3} \mathrm{4} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathrm{5} \mathrm{6} \mathrm{7} \mathrm{8} \mathrm{9}</nowiki></code> | |||
|<math>\mathrm{5} \mathrm{6} \mathrm{7} \mathrm{8} \mathrm{9}\,\!</math> | |||
|- | |||
! colspan="2" | Fraktur typeface | |||
|- | |||
|<code><nowiki>\mathfrak{A} \mathfrak{B} \mathfrak{C} \mathfrak{D} \mathfrak{E} \mathfrak{F} \mathfrak{G}</nowiki></code> | |||
|<math>\mathfrak{A} \mathfrak{B} \mathfrak{C} \mathfrak{D} \mathfrak{E} \mathfrak{F} \mathfrak{G} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{H} \mathfrak{I} \mathfrak{J} \mathfrak{K} \mathfrak{L} \mathfrak{M}</nowiki></code> | |||
|<math>\mathfrak{H} \mathfrak{I} \mathfrak{J} \mathfrak{K} \mathfrak{L} \mathfrak{M} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{N} \mathfrak{O} \mathfrak{P} \mathfrak{Q} \mathfrak{R} \mathfrak{S} \mathfrak{T}</nowiki></code> | |||
|<math>\mathfrak{N} \mathfrak{O} \mathfrak{P} \mathfrak{Q} \mathfrak{R} \mathfrak{S} \mathfrak{T} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{U} \mathfrak{V} \mathfrak{W} \mathfrak{X} \mathfrak{Y} \mathfrak{Z}</nowiki></code> | |||
|<math>\mathfrak{U} \mathfrak{V} \mathfrak{W} \mathfrak{X} \mathfrak{Y} \mathfrak{Z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{a} \mathfrak{b} \mathfrak{c} \mathfrak{d} \mathfrak{e} \mathfrak{f} \mathfrak{g}</nowiki></code> | |||
|<math>\mathfrak{a} \mathfrak{b} \mathfrak{c} \mathfrak{d} \mathfrak{e} \mathfrak{f} \mathfrak{g} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{h} \mathfrak{i} \mathfrak{j} \mathfrak{k} \mathfrak{l} \mathfrak{m}</nowiki></code> | |||
|<math>\mathfrak{h} \mathfrak{i} \mathfrak{j} \mathfrak{k} \mathfrak{l} \mathfrak{m} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{n} \mathfrak{o} \mathfrak{p} \mathfrak{q} \mathfrak{r} \mathfrak{s} \mathfrak{t}</nowiki></code> | |||
|<math>\mathfrak{n} \mathfrak{o} \mathfrak{p} \mathfrak{q} \mathfrak{r} \mathfrak{s} \mathfrak{t} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{u} \mathfrak{v} \mathfrak{w} \mathfrak{x} \mathfrak{y} \mathfrak{z}</nowiki></code> | |||
|<math>\mathfrak{u} \mathfrak{v} \mathfrak{w} \mathfrak{x} \mathfrak{y} \mathfrak{z} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{0} \mathfrak{1} \mathfrak{2} \mathfrak{3} \mathfrak{4}</nowiki></code> | |||
|<math>\mathfrak{0} \mathfrak{1} \mathfrak{2} \mathfrak{3} \mathfrak{4} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathfrak{5} \mathfrak{6} \mathfrak{7} \mathfrak{8} \mathfrak{9}</nowiki></code> | |||
|<math>\mathfrak{5} \mathfrak{6} \mathfrak{7} \mathfrak{8} \mathfrak{9}\,\!</math> | |||
|- | |||
! colspan="2" | Calligraphy/Script | |||
|- | |||
|<code><nowiki>\mathcal{A} \mathcal{B} \mathcal{C} \mathcal{D} \mathcal{E} \mathcal{F} \mathcal{G}</nowiki></code> | |||
|<math>\mathcal{A} \mathcal{B} \mathcal{C} \mathcal{D} \mathcal{E} \mathcal{F} \mathcal{G} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathcal{H} \mathcal{I} \mathcal{J} \mathcal{K} \mathcal{L} \mathcal{M}</nowiki></code> | |||
|<math>\mathcal{H} \mathcal{I} \mathcal{J} \mathcal{K} \mathcal{L} \mathcal{M} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathcal{N} \mathcal{O} \mathcal{P} \mathcal{Q} \mathcal{R} \mathcal{S} \mathcal{T}</nowiki></code> | |||
|<math>\mathcal{N} \mathcal{O} \mathcal{P} \mathcal{Q} \mathcal{R} \mathcal{S} \mathcal{T} \,\!</math> | |||
|- | |||
|<code><nowiki>\mathcal{U} \mathcal{V} \mathcal{W} \mathcal{X} \mathcal{Y} \mathcal{Z}</nowiki></code> | |||
|<math>\mathcal{U} \mathcal{V} \mathcal{W} \mathcal{X} \mathcal{Y} \mathcal{Z}\,\!</math> | |||
|- | |||
! colspan="2" | Hebrew | |||
|- | |||
|<code><nowiki>\aleph \beth \gimel \daleth</nowiki></code> | |||
|<math>\aleph \beth \gimel \daleth\,\!</math> | |||
|} | |||
<table class="wikitable"> | |||
<tr> | |||
<th>Feature</th> | |||
<th>Syntax</th> | |||
<th colspan="2">How it looks rendered</th> | |||
</tr> | |||
<tr> | |||
<td>non-italicised characters</td> | |||
<td>\mbox{abc}</td> | |||
<td><math>\mbox{abc}</math></td> | |||
<td><math>\mbox{abc} \,\!</math></td> | |||
</tr> | |||
<tr> | |||
<td>mixed italics (bad)</td> | |||
<td>\mbox{if} n \mbox{is even}</td> | |||
<td><math>\mbox{if} n \mbox{is even}</math></td> | |||
<td><math>\mbox{if} n \mbox{is even} \,\!</math></td> | |||
</tr> | |||
<tr> | |||
<td>mixed italics (good)</td> | |||
<td>\mbox{if }n\mbox{ is even}</td> | |||
<td><math>\mbox{if }n\mbox{ is even}</math></td> | |||
<td><math>\mbox{if }n\mbox{ is even} \,\!</math></td> | |||
</tr> | |||
<tr> | |||
<td>mixed italics (more legible: ~ is a non-breaking space, while "\ " forces a space)</td> | |||
<td>\mbox{if}~n\ \mbox{is even}</td> | |||
<td><math>\mbox{if}~n\ \mbox{is even}</math></td> | |||
<td><math>\mbox{if}~n\ \mbox{is even} \,\!</math></td> | |||
</tr> | |||
</table> | |||
== Alternatives == | == Alternatives == | ||
| Line 50: | Line 646: | ||
* Images files may be unnecessary large. | * Images files may be unnecessary large. | ||
* Files can only be uploaded by registered users. | * Files can only be uploaded by registered users. | ||
== Comparison == | |||
=== Image === | |||
<div style="border:1px solid #aaaaaa; padding:1em;"> | |||
[[Image:Equation-gn-transition-angle-brackets-3.png]] | |||
</div> | |||
<pre> | |||
[[Image:Equation-gn-transition-angle-brackets-3.png]] | |||
</pre> | |||
=== Wiki markup === | |||
<div style="border:1px solid #aaaaaa; padding:1em;"> | |||
Z<sub>5</sub> = < {l<sub>7</sub>, m<sub>4</sub>}, {l<sub>8</sub>, m<sub>5</sub>}, M<sub>5</sub>, Λ(l<sub>7</sub>, m<sub>3</sub>) > | |||
: where | |||
{{index-matrix/start | |||
|matrix-id = M<sub>5</sub> | |||
|columns = 2 | |||
|1 = l<sub>8</sub> | |||
|2 = m<sub>5</sub> | |||
}} | |||
{{index-matrix/row-predic | |||
|columns= 2 | |||
|row-id = l<sub>7</sub> | |||
|1 = true | |||
|2 = false | |||
}} | |||
{{index-matrix/row-predic | |||
|columns= 2 | |||
|row-id = m<sub>4</sub> | |||
|1 = W<sub>4,8</sub> | |||
|2 = W<sub>4,5</sub> | |||
}} | |||
{{index-matrix/end}} | |||
</div> | |||
<pre> | |||
Z<sub>5</sub> = < {l<sub>7</sub>, m<sub>4</sub>}, {l<sub>8</sub>, m<sub>5</sub>}, IM<sub>P</sub>, Λ(l<sub>7</sub>, m<sub>3</sub>) > | |||
: where | |||
{{index-matrix/start | |||
|matrix-id = IM<sub>P</sub> | |||
|columns = 2 | |||
|1 = l<sub>8</sub> | |||
|2 = m<sub>5</sub> | |||
}} | |||
{{index-matrix/row-predic | |||
|columns= 2 | |||
|row-id = l<sub>7</sub> | |||
|1 = true | |||
|2 = false | |||
}} | |||
{{index-matrix/row-predic | |||
|columns= 2 | |||
|row-id = m<sub>4</sub> | |||
|1 = W<sub>4,8</sub> | |||
|2 = W<sub>4,5</sub> | |||
}} | |||
{{index-matrix/end}} | |||
</pre> | |||
=== TeX === | |||
<div style="border:1px solid #aaaaaa; padding:1em;"> | |||
<math>Z_5 = \big< \{ l_7, m_4 \}, \{ l_8, m_5 \}, | |||
\begin{array}{c|c c} & l_8 & m_5 \\ | |||
\hline | |||
l_7 & true & false \\ | |||
m_4 & W_{4,8} & W_{4,5} \\ | |||
\end{array}, | |||
\land (l_7, m_3) \big></math> | |||
</div> | |||
<pre> | |||
<math> | |||
Z_5 = \big< \{ l_7, m_4 \}, \{ l_8, m_5 \}, | |||
\begin{array}{c|c c} & l_8 & m_5 \\ | |||
\hline | |||
l_7 & true & false \\ | |||
m_4 & W_{4,8} & W_{4,5} \\ | |||
\end{array}, | |||
\land (l_7, m_3) \big> | |||
</math> | |||
</pre> | |||
== See also == | == See also == | ||
* [[Help:Formulas/Formulas in MS Word]] | |||
* [http://meta.wikimedia.org/wiki/Help:Displaying_a_formula Help:Displaying a formula] on Meta-Wikipedia | |||
* [http://en.wikipedia.org/wiki/Wikipedia:Manual_of_Style_(mathematics) Manual of Style (mathematics)] on English Wikipedia | |||
* [[Help:Contents]] for other help pages | |||
[[Category:Help pages|{{PAGENAME}}]] | [[Category:Help pages|{{PAGENAME}}]] | ||
Latest revision as of 14:09, 24 October 2008
| First steps | Page editing | Page management | Namespaces | Tools and settings |
| Starting a new page • Edit mode • Text formatting • Formulas • Tables • Images • Categories • Templates • References • Subpages | ||||
Formulas on a wiki like Ifigenia can be represented in three ways, depending on the formula complexity and tools used:
- Unicode characters - for simple formulas, of course :-)
- Images - for formulas of any complexity, created as an image file (preferably
.pngor.gif) and uploaded locally. - TeX code - for formulas of any complexity - from very simple to extremely sophisticated
Maybe, for the users of Ifigenia TeX-coded formulas may turn out to be the most natural ones. They allow relatively good integration with other TeX documents and they can be further saved as image files, for the sake of integration with MS Word documents.
Formulas in TeX
In the wiki websites, TeX-formulas are distinguished from the rest of the text by enclosing them with the tags <math> </math>. A handy way is to click the Math button ![]() and then write between the tags.
and then write between the tags.
On Ifigenia, the TeX formulas are rendered using a public mimeTeX web service, so the process may be a bit slower, about 1 second per 1 <math>-call.
Rendered TeX formulas can be stored on the hard disk as images in .gif format (default) or .png (optional).
Here is a reference list for the various TeX commands in use.
Functions, symbols, special characters
Accents/Diacritics | |
|---|---|
\acute{a} \grave{a} \hat{a} \tilde{a} \breve{a}
|
[math]\displaystyle{ \acute{a} \grave{a} \hat{a} \tilde{a} \breve{a}\,\! }[/math] |
\check{a} \bar{a} \ddot{a} \dot{a}
|
[math]\displaystyle{ \check{a} \bar{a} \ddot{a} \dot{a}\,\! }[/math] |
Standard functions | |
\sin a \cos b \tan c
|
[math]\displaystyle{ \sin a \cos b \tan c\,\! }[/math] |
\sec d \csc e \cot f
|
[math]\displaystyle{ \sec d \csc e \cot f\,\! }[/math] |
\arcsin h \arccos i \arctan j
|
[math]\displaystyle{ \arcsin h \arccos i \arctan j\,\! }[/math] |
\sinh k \cosh l \tanh m \coth n
|
[math]\displaystyle{ \sinh k \cosh l \tanh m \coth n\,\! }[/math] |
\operatorname{sh}\,o\,\operatorname{ch}\,p\,\operatorname{th}\,q
|
[math]\displaystyle{ \operatorname{sh}\,o\,\operatorname{ch}\,p\,\operatorname{th}\,q\,\! }[/math] |
\operatorname{arsinh}\,r\,\operatorname{arcosh}\,s\,\operatorname{artanh}\,t
|
[math]\displaystyle{ \operatorname{arsinh}\,r\,\operatorname{arcosh}\,s\,\operatorname{artanh}\,t\,\! }[/math] |
\lim u \limsup v \liminf w \min x \max y
|
[math]\displaystyle{ \lim u \limsup v \liminf w \min x \max y\,\! }[/math] |
\inf z \sup a \exp b \ln c \lg d \log e \log_{10} f \ker g
|
[math]\displaystyle{ \inf z \sup a \exp b \ln c \lg d \log e \log_{10} f \ker g\,\! }[/math] |
\deg h \gcd i \Pr j \det k \hom l \arg m \dim n
|
[math]\displaystyle{ \deg h \gcd i \Pr j \det k \hom l \arg m \dim n\,\! }[/math] |
Modular arithmetic | |
s_k \equiv 0 \pmod{m}
|
[math]\displaystyle{ s_k \equiv 0 \pmod{m}\,\! }[/math] |
a\,\bmod\,b
|
[math]\displaystyle{ a\,\bmod\,b\,\! }[/math] |
Derivatives | |
\nabla \, \partial x \, dx \, \dot x \, \ddot y\, dy/dx\, \frac{dy}{dx}\, \frac{\partial^2 y}{\partial x_1\,\partial x_2}
|
[math]\displaystyle{ \nabla \, \partial x \, dx \, \dot x \, \ddot y\, dy/dx\, \frac{dy}{dx}\, \frac{\partial^2 y}{\partial x_1\,\partial x_2} }[/math] |
Sets | |
\forall \exists \empty \emptyset \varnothing
|
[math]\displaystyle{ \forall \exists \empty \emptyset \varnothing\,\! }[/math] |
\in \ni \not \in \notin \subset \subseteq \supset \supseteq
|
[math]\displaystyle{ \in \ni \not \in \notin \subset \subseteq \supset \supseteq\,\! }[/math] |
\cap \bigcap \cup \bigcup \biguplus \setminus \smallsetminus
|
[math]\displaystyle{ \cap \bigcap \cup \bigcup \biguplus \setminus \smallsetminus\,\! }[/math] |
\sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup
|
[math]\displaystyle{ \sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup\,\! }[/math] |
Operators | |
+ \oplus \bigoplus \pm \mp -
|
[math]\displaystyle{ + \oplus \bigoplus \pm \mp - \,\! }[/math] |
\times \otimes \bigotimes \cdot \circ \bullet \bigodot
|
[math]\displaystyle{ \times \otimes \bigotimes \cdot \circ \bullet \bigodot\,\! }[/math] |
\star * / \div \frac{1}{2}
|
[math]\displaystyle{ \star * / \div \frac{1}{2}\,\! }[/math] |
Logic | |
\land (or \and) \wedge \bigwedge \bar{q} \to p
|
[math]\displaystyle{ \land \wedge \bigwedge \bar{q} \to p\,\! }[/math] |
\lor \vee \bigvee \lnot \neg q \And
|
[math]\displaystyle{ \lor \vee \bigvee \lnot \neg q \And\,\! }[/math] |
Root | |
\sqrt{2} \sqrt[n]{x}
|
[math]\displaystyle{ \sqrt{2} \sqrt[n]{x}\,\! }[/math] |
Relations | |
\sim \approx \simeq \cong \dot= \overset{\underset{\mathrm{def}}{}}{=}
|
[math]\displaystyle{ \sim \approx \simeq \cong \dot= \overset{\underset{\mathrm{def}}{}}{=}\,\! }[/math] |
\le < \ll \gg \ge > \equiv \not\equiv \ne \mbox{or} \neq \propto
|
[math]\displaystyle{ \le \lt \ll \gg \ge \gt \equiv \not\equiv \ne \mbox{or} \neq \propto\,\! }[/math] |
Geometric | |
\Diamond \Box \triangle \angle \perp \mid \nmid \| 45^\circ
|
[math]\displaystyle{ \Diamond \, \Box \, \triangle \, \angle \perp \, \mid \; \nmid \, \| 45^\circ\,\! }[/math] |
Arrows | |
\leftarrow (or \gets) \rightarrow (or \to) \nleftarrow \nrightarrow \leftrightarrow \nleftrightarrow \longleftarrow \longrightarrow \longleftrightarrow
|
[math]\displaystyle{ \leftarrow \rightarrow \nleftarrow \not\to \leftrightarrow \nleftrightarrow \longleftarrow \longrightarrow \longleftrightarrow \,\! }[/math] |
\Leftarrow \Rightarrow \nLeftarrow \nRightarrow \Leftrightarrow \nLeftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow (or \iff)
|
[math]\displaystyle{ \Leftarrow \Rightarrow \nLeftarrow \nRightarrow \Leftrightarrow \nLeftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow \,\! }[/math] |
\uparrow \downarrow \updownarrow \Uparrow \Downarrow \Updownarrow \nearrow \searrow \swarrow \nwarrow
|
[math]\displaystyle{ \uparrow \downarrow \updownarrow \Uparrow \Downarrow \Updownarrow \nearrow \searrow \swarrow \nwarrow \,\! }[/math] |
\rightharpoonup \rightharpoondown \leftharpoonup \leftharpoondown \upharpoonleft \upharpoonright \downharpoonleft \downharpoonright \rightleftharpoons \leftrightharpoons
|
[math]\displaystyle{ \rightharpoonup \rightharpoondown \leftharpoonup \leftharpoondown \upharpoonleft \upharpoonright \downharpoonleft \downharpoonright \rightleftharpoons \leftrightharpoons \,\! }[/math] |
\curvearrowleft \circlearrowleft \Lsh \upuparrows \rightrightarrows \rightleftarrows \Rrightarrow \rightarrowtail \looparrowright
|
[math]\displaystyle{ \curvearrowleft \circlearrowleft \Lsh \upuparrows \rightrightarrows \rightleftarrows \Rrightarrow \rightarrowtail \looparrowright \,\! }[/math] |
\curvearrowright \circlearrowright \Rsh \downdownarrows \leftleftarrows \leftrightarrows \Lleftarrow \leftarrowtail \looparrowleft
|
[math]\displaystyle{ \curvearrowright \circlearrowright \Rsh \downdownarrows \leftleftarrows \leftrightarrows \Lleftarrow \leftarrowtail \looparrowleft \,\! }[/math] |
\mapsto \longmapsto \hookrightarrow \hookleftarrow \multimap \leftrightsquigarrow \rightsquigarrow
|
[math]\displaystyle{ \mapsto \longmapsto \hookrightarrow \hookleftarrow \multimap \leftrightsquigarrow \rightsquigarrow \,\! }[/math] |
Special | |
\And \eth \S \P \% \dagger \ddagger \ldots \cdots
|
[math]\displaystyle{ \And \eth \S \P \% \dagger \ddagger \ldots \cdots\,\! }[/math] |
\smile \frown \wr \triangleleft \triangleright \infty \bot \top
|
[math]\displaystyle{ \smile \frown \wr \triangleleft \triangleright \infty \bot \top\,\! }[/math] |
\vdash \vDash \Vdash \models \lVert \rVert \imath \hbar
|
[math]\displaystyle{ \vdash \vDash \Vdash \models \lVert \rVert \imath \hbar\,\! }[/math] |
\ell \mho \Finv \Re \Im \wp \complement
|
[math]\displaystyle{ \ell \mho \Finv \Re \Im \wp \complement\,\! }[/math] |
\diamondsuit \heartsuit \clubsuit \spadesuit \Game \flat \natural \sharp
|
[math]\displaystyle{ \diamondsuit \heartsuit \clubsuit \spadesuit \Game \flat \natural \sharp\,\! }[/math] |
Unsorted (new stuff) | |
\vartriangle \triangledown \lozenge \circledS \measuredangle \nexists \Bbbk \backprime \blacktriangle \blacktriangledown
|
[math]\displaystyle{ \vartriangle \triangledown \lozenge \circledS \measuredangle \nexists \Bbbk \backprime \blacktriangle \blacktriangledown }[/math] |
\blacksquare \blacklozenge \bigstar \sphericalangle \diagup \diagdown \dotplus \Cap \Cup \barwedge
|
[math]\displaystyle{ \blacksquare \blacklozenge \bigstar \sphericalangle \diagup \diagdown \dotplus \Cap \Cup \barwedge }[/math] |
\veebar \doublebarwedge \boxminus \boxtimes \boxdot \boxplus \divideontimes \ltimes \rtimes \leftthreetimes
|
[math]\displaystyle{ \veebar \doublebarwedge \boxminus \boxtimes \boxdot \boxplus \divideontimes \ltimes \rtimes \leftthreetimes }[/math] |
\rightthreetimes \curlywedge \curlyvee \circleddash \circledast \circledcirc \centerdot \intercal \leqq \leqslant
|
[math]\displaystyle{ \rightthreetimes \curlywedge \curlyvee \circleddash \circledast \circledcirc \centerdot \intercal \leqq \leqslant }[/math] |
\eqslantless \lessapprox \approxeq \lessdot \lll \lessgtr \lesseqgtr \lesseqqgtr \doteqdot \risingdotseq
|
[math]\displaystyle{ \eqslantless \lessapprox \approxeq \lessdot \lll \lessgtr \lesseqgtr \lesseqqgtr \doteqdot \risingdotseq }[/math] |
\fallingdotseq \backsim \backsimeq \subseteqq \Subset \preccurlyeq \curlyeqprec \precsim \precapprox \vartriangleleft
|
[math]\displaystyle{ \fallingdotseq \backsim \backsimeq \subseteqq \Subset \preccurlyeq \curlyeqprec \precsim \precapprox \vartriangleleft }[/math] |
\Vvdash \bumpeq \Bumpeq \geqq \geqslant \eqslantgtr \gtrsim \gtrapprox \eqsim \gtrdot
|
[math]\displaystyle{ \Vvdash \bumpeq \Bumpeq \geqq \geqslant \eqslantgtr \gtrsim \gtrapprox \eqsim \gtrdot }[/math] |
\ggg \gtrless \gtreqless \gtreqqless \eqcirc \circeq \triangleq \thicksim \thickapprox \supseteqq
|
[math]\displaystyle{ \ggg \gtrless \gtreqless \gtreqqless \eqcirc \circeq \triangleq \thicksim \thickapprox \supseteqq }[/math] |
\Supset \succcurlyeq \curlyeqsucc \succsim \succapprox \vartriangleright \shortmid \shortparallel \between \pitchfork
|
[math]\displaystyle{ \Supset \succcurlyeq \curlyeqsucc \succsim \succapprox \vartriangleright \shortmid \shortparallel \between \pitchfork }[/math] |
\varpropto \blacktriangleleft \therefore \backepsilon \blacktriangleright \because \nleqslant \nleqq \lneq \lneqq
|
[math]\displaystyle{ \varpropto \blacktriangleleft \therefore \backepsilon \blacktriangleright \because \nleqslant \nleqq \lneq \lneqq }[/math] |
\lvertneqq \lnsim \lnapprox \nprec \npreceq \precneqq \precnsim \precnapprox \nsim \nshortmid
|
[math]\displaystyle{ \lvertneqq \lnsim \lnapprox \nprec \npreceq \precneqq \precnsim \precnapprox \nsim \nshortmid }[/math] |
\nvdash \nVdash \ntriangleleft \ntrianglelefteq \nsubseteq \nsubseteqq \varsubsetneq \subsetneqq \varsubsetneqq \ngtr
|
[math]\displaystyle{ \nvdash \nVdash \ntriangleleft \ntrianglelefteq \nsubseteq \nsubseteqq \varsubsetneq \subsetneqq \varsubsetneqq \ngtr }[/math] |
\subsetneq
|
[math]\displaystyle{ \subsetneq }[/math] |
\ngeqslant \ngeqq \gneq \gneqq \gvertneqq \gnsim \gnapprox \nsucc \nsucceq \succneqq
|
[math]\displaystyle{ \ngeqslant \ngeqq \gneq \gneqq \gvertneqq \gnsim \gnapprox \nsucc \nsucceq \succneqq }[/math] |
\succnsim \succnapprox \ncong \nshortparallel \nparallel \nvDash \nVDash \ntriangleright \ntrianglerighteq \nsupseteq
|
[math]\displaystyle{ \succnsim \succnapprox \ncong \nshortparallel \nparallel \nvDash \nVDash \ntriangleright \ntrianglerighteq \nsupseteq }[/math] |
\nsupseteqq \varsupsetneq \supsetneqq \varsupsetneqq
|
[math]\displaystyle{ \nsupseteqq \varsupsetneq \supsetneqq \varsupsetneqq }[/math] |
\jmath \surd \ast \uplus \diamond \bigtriangleup \bigtriangledown \ominus
|
[math]\displaystyle{ \jmath \surd \ast \uplus \diamond \bigtriangleup \bigtriangledown \ominus\,\! }[/math] |
\oslash \odot \bigcirc \amalg \prec \succ \preceq \succeq
|
[math]\displaystyle{ \oslash \odot \bigcirc \amalg \prec \succ \preceq \succeq\,\! }[/math] |
\dashv \asymp \doteq \parallel
|
[math]\displaystyle{ \dashv \asymp \doteq \parallel\,\! }[/math] |
\ulcorner \urcorner \llcorner \lrcorner
|
[math]\displaystyle{ \ulcorner \urcorner \llcorner \lrcorner }[/math] |
Subscripts, superscripts, integrals
| Feature | Syntax | How it looks rendered | |
|---|---|---|---|
| HTML | PNG | ||
| Superscript | a^2 |
[math]\displaystyle{ a^2 }[/math] | [math]\displaystyle{ a^2 \,\! }[/math] |
| Subscript | a_2 |
[math]\displaystyle{ a_2 }[/math] | [math]\displaystyle{ a_2 \,\! }[/math] |
| Grouping | a^{2+2} |
[math]\displaystyle{ a^{2+2} }[/math] | [math]\displaystyle{ a^{2+2}\,\! }[/math] |
a_{i,j} |
[math]\displaystyle{ a_{i,j} }[/math] | [math]\displaystyle{ a_{i,j}\,\! }[/math] | |
| Combining sub & super | x_2^3 |
[math]\displaystyle{ x_2^3 }[/math] | |
| Super super | 10^{10^{ \,\!{8} } |
[math]\displaystyle{ 10^{10^{ \,\! 8 } } }[/math] | |
| Super super | 10^{10^{ \overset{8}{} }} |
[math]\displaystyle{ 10^{10^{ \overset{8}{} }} }[/math] | |
| Super super (wrong in HTML in some browsers) | 10^{10^8} |
[math]\displaystyle{ 10^{10^8} }[/math] | |
| Preceding and/or Additional sub & super | \sideset{_1^2}{_3^4}\prod_a^b |
[math]\displaystyle{ \sideset{_1^2}{_3^4}\prod_a^b }[/math] | |
{}_1^2\!\Omega_3^4 |
[math]\displaystyle{ {}_1^2\!\Omega_3^4 }[/math] | ||
| Stacking | \overset{\alpha}{\omega} |
[math]\displaystyle{ \overset{\alpha}{\omega} }[/math] | |
\underset{\alpha}{\omega} |
[math]\displaystyle{ \underset{\alpha}{\omega} }[/math] | ||
\overset{\alpha}{\underset{\gamma}{\omega}} |
[math]\displaystyle{ \overset{\alpha}{\underset{\gamma}{\omega}} }[/math] | ||
\stackrel{\alpha}{\omega} |
[math]\displaystyle{ \stackrel{\alpha}{\omega} }[/math] | ||
| Derivative (forced PNG) | x', y'', f', f''\! |
[math]\displaystyle{ x', y'', f', f''\! }[/math] | |
| Derivative (f in italics may overlap primes in HTML) | x', y'', f', f'' |
[math]\displaystyle{ x', y'', f', f'' }[/math] | [math]\displaystyle{ x', y'', f', f''\! }[/math] |
| Derivative (wrong in HTML) | x^\prime, y^{\prime\prime} |
[math]\displaystyle{ x^\prime, y^{\prime\prime} }[/math] | [math]\displaystyle{ x^\prime, y^{\prime\prime}\,\! }[/math] |
| Derivative (wrong in PNG) | x\prime, y\prime\prime |
[math]\displaystyle{ x\prime, y\prime\prime }[/math] | [math]\displaystyle{ x\prime, y\prime\prime\,\! }[/math] |
| Derivative dots | \dot{x}, \ddot{x} |
[math]\displaystyle{ \dot{x}, \ddot{x} }[/math] | |
| Underlines, overlines, vectors | \hat a \ \bar b \ \vec c |
[math]\displaystyle{ \hat a \ \bar b \ \vec c }[/math] | |
\overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f} |
[math]\displaystyle{ \overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f} }[/math] | ||
\overline{g h i} \ \underline{j k l} |
[math]\displaystyle{ \overline{g h i} \ \underline{j k l} }[/math] | ||
| Arrows | A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C |
[math]\displaystyle{ A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C }[/math] | |
| Overbraces | \overbrace{ 1+2+\cdots+100 }^{5050} |
[math]\displaystyle{ \overbrace{ 1+2+\cdots+100 }^{5050} }[/math] | |
| Underbraces | \underbrace{ a+b+\cdots+z }_{26} |
[math]\displaystyle{ \underbrace{ a+b+\cdots+z }_{26} }[/math] | |
| Sum | \sum_{k=1}^N k^2 |
[math]\displaystyle{ \sum_{k=1}^N k^2 }[/math] | |
Sum (force \textstyle) |
\textstyle \sum_{k=1}^N k^2 |
[math]\displaystyle{ \textstyle \sum_{k=1}^N k^2 }[/math] | |
| Product | \prod_{i=1}^N x_i |
[math]\displaystyle{ \prod_{i=1}^N x_i }[/math] | |
Product (force \textstyle) |
\textstyle \prod_{i=1}^N x_i |
[math]\displaystyle{ \textstyle \prod_{i=1}^N x_i }[/math] | |
| Coproduct | \coprod_{i=1}^N x_i |
[math]\displaystyle{ \coprod_{i=1}^N x_i }[/math] | |
Coproduct (force \textstyle) |
\textstyle \coprod_{i=1}^N x_i |
[math]\displaystyle{ \textstyle \coprod_{i=1}^N x_i }[/math] | |
| Limit | \lim_{n \to \infty}x_n |
[math]\displaystyle{ \lim_{n \to \infty}x_n }[/math] | |
Limit (force \textstyle) |
\textstyle \lim_{n \to \infty}x_n |
[math]\displaystyle{ \textstyle \lim_{n \to \infty}x_n }[/math] | |
| Integral | \int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx |
[math]\displaystyle{ \int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx }[/math] | |
| Integral (alternate limits style) | \int_{1}^{3}\frac{e^3/x}{x^2}\, dx |
[math]\displaystyle{ \int_{1}^{3}\frac{e^3/x}{x^2}\, dx }[/math] | |
Integral (force \textstyle) |
\textstyle \int\limits_{-N}^{N} e^x\, dx |
[math]\displaystyle{ \textstyle \int\limits_{-N}^{N} e^x\, dx }[/math] | |
Integral (force \textstyle, alternate limits style) |
\textstyle \int_{-N}^{N} e^x\, dx |
[math]\displaystyle{ \textstyle \int_{-N}^{N} e^x\, dx }[/math] | |
| Double integral | \iint\limits_D \, dx\,dy |
[math]\displaystyle{ \iint\limits_D \, dx\,dy }[/math] | |
| Triple integral | \iiint\limits_E \, dx\,dy\,dz |
[math]\displaystyle{ \iiint\limits_E \, dx\,dy\,dz }[/math] | |
| Quadruple integral | \iiiint\limits_F \, dx\,dy\,dz\,dt |
[math]\displaystyle{ \iiiint\limits_F \, dx\,dy\,dz\,dt }[/math] | |
| Line or path integral | \int_C x^3\, dx + 4y^2\, dy |
[math]\displaystyle{ \int_C x^3\, dx + 4y^2\, dy }[/math] | |
| Closed line or path integral | \oint_C x^3\, dx + 4y^2\, dy |
[math]\displaystyle{ \oint_C x^3\, dx + 4y^2\, dy }[/math] | |
| Intersections | \bigcap_1^n p |
[math]\displaystyle{ \bigcap_1^n p }[/math] | |
| Unions | \bigcup_1^k p |
[math]\displaystyle{ \bigcup_1^k p }[/math] | |
Alphabets and typefaces
| Greek alphabet | |
|---|---|
\Alpha \Beta \Gamma \Delta \Epsilon \Zeta
|
[math]\displaystyle{ \Alpha \Beta \Gamma \Delta \Epsilon \Zeta \,\! }[/math] |
\Eta \Theta \Iota \Kappa \Lambda \Mu
|
[math]\displaystyle{ \Eta \Theta \Iota \Kappa \Lambda \Mu \,\! }[/math] |
\Nu \Xi \Pi \Rho \Sigma \Tau
|
[math]\displaystyle{ \Nu \Xi \Pi \Rho \Sigma \Tau\,\! }[/math] |
\Upsilon \Phi \Chi \Psi \Omega
|
[math]\displaystyle{ \Upsilon \Phi \Chi \Psi \Omega \,\! }[/math] |
\alpha \beta \gamma \delta \epsilon \zeta
|
[math]\displaystyle{ \alpha \beta \gamma \delta \epsilon \zeta \,\! }[/math] |
\eta \theta \iota \kappa \lambda \mu
|
[math]\displaystyle{ \eta \theta \iota \kappa \lambda \mu \,\! }[/math] |
\nu \xi \pi \rho \sigma \tau
|
[math]\displaystyle{ \nu \xi \pi \rho \sigma \tau \,\! }[/math] |
\upsilon \phi \chi \psi \omega
|
[math]\displaystyle{ \upsilon \phi \chi \psi \omega \,\! }[/math] |
\varepsilon \digamma \vartheta \varkappa
|
[math]\displaystyle{ \varepsilon \digamma \vartheta \varkappa \,\! }[/math] |
\varpi \varrho \varsigma \varphi
|
[math]\displaystyle{ \varpi \varrho \varsigma \varphi\,\! }[/math] |
| Blackboard Bold/Scripts | |
\mathbb{A} \mathbb{B} \mathbb{C} \mathbb{D} \mathbb{E} \mathbb{F} \mathbb{G}
|
[math]\displaystyle{ \mathbb{A} \mathbb{B} \mathbb{C} \mathbb{D} \mathbb{E} \mathbb{F} \mathbb{G} \,\! }[/math] |
\mathbb{H} \mathbb{I} \mathbb{J} \mathbb{K} \mathbb{L} \mathbb{M}
|
[math]\displaystyle{ \mathbb{H} \mathbb{I} \mathbb{J} \mathbb{K} \mathbb{L} \mathbb{M} \,\! }[/math] |
\mathbb{N} \mathbb{O} \mathbb{P} \mathbb{Q} \mathbb{R} \mathbb{S} \mathbb{T}
|
[math]\displaystyle{ \mathbb{N} \mathbb{O} \mathbb{P} \mathbb{Q} \mathbb{R} \mathbb{S} \mathbb{T} \,\! }[/math] |
\mathbb{U} \mathbb{V} \mathbb{W} \mathbb{X} \mathbb{Y} \mathbb{Z}
|
[math]\displaystyle{ \mathbb{U} \mathbb{V} \mathbb{W} \mathbb{X} \mathbb{Y} \mathbb{Z}\,\! }[/math] |
| boldface (vectors) | |
\mathbf{A} \mathbf{B} \mathbf{C} \mathbf{D} \mathbf{E} \mathbf{F} \mathbf{G}
|
[math]\displaystyle{ \mathbf{A} \mathbf{B} \mathbf{C} \mathbf{D} \mathbf{E} \mathbf{F} \mathbf{G} \,\! }[/math] |
\mathbf{H} \mathbf{I} \mathbf{J} \mathbf{K} \mathbf{L} \mathbf{M}
|
[math]\displaystyle{ \mathbf{H} \mathbf{I} \mathbf{J} \mathbf{K} \mathbf{L} \mathbf{M} \,\! }[/math] |
\mathbf{N} \mathbf{O} \mathbf{P} \mathbf{Q} \mathbf{R} \mathbf{S} \mathbf{T}
|
[math]\displaystyle{ \mathbf{N} \mathbf{O} \mathbf{P} \mathbf{Q} \mathbf{R} \mathbf{S} \mathbf{T} \,\! }[/math] |
\mathbf{U} \mathbf{V} \mathbf{W} \mathbf{X} \mathbf{Y} \mathbf{Z}
|
[math]\displaystyle{ \mathbf{U} \mathbf{V} \mathbf{W} \mathbf{X} \mathbf{Y} \mathbf{Z} \,\! }[/math] |
\mathbf{a} \mathbf{b} \mathbf{c} \mathbf{d} \mathbf{e} \mathbf{f} \mathbf{g}
|
[math]\displaystyle{ \mathbf{a} \mathbf{b} \mathbf{c} \mathbf{d} \mathbf{e} \mathbf{f} \mathbf{g} \,\! }[/math] |
\mathbf{h} \mathbf{i} \mathbf{j} \mathbf{k} \mathbf{l} \mathbf{m}
|
[math]\displaystyle{ \mathbf{h} \mathbf{i} \mathbf{j} \mathbf{k} \mathbf{l} \mathbf{m} \,\! }[/math] |
\mathbf{n} \mathbf{o} \mathbf{p} \mathbf{q} \mathbf{r} \mathbf{s} \mathbf{t}
|
[math]\displaystyle{ \mathbf{n} \mathbf{o} \mathbf{p} \mathbf{q} \mathbf{r} \mathbf{s} \mathbf{t} \,\! }[/math] |
\mathbf{u} \mathbf{v} \mathbf{w} \mathbf{x} \mathbf{y} \mathbf{z}
|
[math]\displaystyle{ \mathbf{u} \mathbf{v} \mathbf{w} \mathbf{x} \mathbf{y} \mathbf{z} \,\! }[/math] |
\mathbf{0} \mathbf{1} \mathbf{2} \mathbf{3} \mathbf{4}
|
[math]\displaystyle{ \mathbf{0} \mathbf{1} \mathbf{2} \mathbf{3} \mathbf{4} \,\! }[/math] |
\mathbf{5} \mathbf{6} \mathbf{7} \mathbf{8} \mathbf{9}
|
[math]\displaystyle{ \mathbf{5} \mathbf{6} \mathbf{7} \mathbf{8} \mathbf{9}\,\! }[/math] |
| Boldface (greek) | |
\boldsymbol{\Alpha} \boldsymbol{\Beta} \boldsymbol{\Gamma} \boldsymbol{\Delta} \boldsymbol{\Epsilon} \boldsymbol{\Zeta}
|
[math]\displaystyle{ \boldsymbol{\Alpha} \boldsymbol{\Beta} \boldsymbol{\Gamma} \boldsymbol{\Delta} \boldsymbol{\Epsilon} \boldsymbol{\Zeta} \,\! }[/math] |
\boldsymbol{\Eta} \boldsymbol{\Theta} \boldsymbol{\Iota} \boldsymbol{\Kappa} \boldsymbol{\Lambda} \boldsymbol{\Mu}
|
[math]\displaystyle{ \boldsymbol{\Eta} \boldsymbol{\Theta} \boldsymbol{\Iota} \boldsymbol{\Kappa} \boldsymbol{\Lambda} \boldsymbol{\Mu}\,\! }[/math] |
\boldsymbol{\Nu} \boldsymbol{\Xi} \boldsymbol{\Pi} \boldsymbol{\Rho} \boldsymbol{\Sigma} \boldsymbol{\Tau}
|
[math]\displaystyle{ \boldsymbol{\Nu} \boldsymbol{\Xi} \boldsymbol{\Pi} \boldsymbol{\Rho} \boldsymbol{\Sigma} \boldsymbol{\Tau}\,\! }[/math] |
\boldsymbol{\Upsilon} \boldsymbol{\Phi} \boldsymbol{\Chi} \boldsymbol{\Psi} \boldsymbol{\Omega}
|
[math]\displaystyle{ \boldsymbol{\Upsilon} \boldsymbol{\Phi} \boldsymbol{\Chi} \boldsymbol{\Psi} \boldsymbol{\Omega}\,\! }[/math] |
\boldsymbol{\alpha} \boldsymbol{\beta} \boldsymbol{\gamma} \boldsymbol{\delta} \boldsymbol{\epsilon} \boldsymbol{\zeta}
|
[math]\displaystyle{ \boldsymbol{\alpha} \boldsymbol{\beta} \boldsymbol{\gamma} \boldsymbol{\delta} \boldsymbol{\epsilon} \boldsymbol{\zeta}\,\! }[/math] |
\boldsymbol{\eta} \boldsymbol{\theta} \boldsymbol{\iota} \boldsymbol{\kappa} \boldsymbol{\lambda} \boldsymbol{\mu}
|
[math]\displaystyle{ \boldsymbol{\eta} \boldsymbol{\theta} \boldsymbol{\iota} \boldsymbol{\kappa} \boldsymbol{\lambda} \boldsymbol{\mu}\,\! }[/math] |
\boldsymbol{\nu} \boldsymbol{\xi} \boldsymbol{\pi} \boldsymbol{\rho} \boldsymbol{\sigma} \boldsymbol{\tau}
|
[math]\displaystyle{ \boldsymbol{\nu} \boldsymbol{\xi} \boldsymbol{\pi} \boldsymbol{\rho} \boldsymbol{\sigma} \boldsymbol{\tau}\,\! }[/math] |
\boldsymbol{\upsilon} \boldsymbol{\phi} \boldsymbol{\chi} \boldsymbol{\psi} \boldsymbol{\omega}
|
[math]\displaystyle{ \boldsymbol{\upsilon} \boldsymbol{\phi} \boldsymbol{\chi} \boldsymbol{\psi} \boldsymbol{\omega}\,\! }[/math] |
\boldsymbol{\varepsilon} \boldsymbol{\digamma} \boldsymbol{\vartheta} \boldsymbol{\varkappa}
|
[math]\displaystyle{ \boldsymbol{\varepsilon} \boldsymbol{\digamma} \boldsymbol{\vartheta} \boldsymbol{\varkappa} \,\! }[/math] |
\boldsymbol{\varpi} \boldsymbol{\varrho} \boldsymbol{\varsigma} \boldsymbol{\varphi}
|
[math]\displaystyle{ \boldsymbol{\varpi} \boldsymbol{\varrho} \boldsymbol{\varsigma} \boldsymbol{\varphi}\,\! }[/math] |
| Italics | |
\mathit{A} \mathit{B} \mathit{C} \mathit{D} \mathit{E} \mathit{F} \mathit{G}
|
[math]\displaystyle{ \mathit{A} \mathit{B} \mathit{C} \mathit{D} \mathit{E} \mathit{F} \mathit{G} \,\! }[/math] |
\mathit{H} \mathit{I} \mathit{J} \mathit{K} \mathit{L} \mathit{M}
|
[math]\displaystyle{ \mathit{H} \mathit{I} \mathit{J} \mathit{K} \mathit{L} \mathit{M} \,\! }[/math] |
\mathit{N} \mathit{O} \mathit{P} \mathit{Q} \mathit{R} \mathit{S} \mathit{T}
|
[math]\displaystyle{ \mathit{N} \mathit{O} \mathit{P} \mathit{Q} \mathit{R} \mathit{S} \mathit{T} \,\! }[/math] |
\mathit{U} \mathit{V} \mathit{W} \mathit{X} \mathit{Y} \mathit{Z}
|
[math]\displaystyle{ \mathit{U} \mathit{V} \mathit{W} \mathit{X} \mathit{Y} \mathit{Z} \,\! }[/math] |
\mathit{a} \mathit{b} \mathit{c} \mathit{d} \mathit{e} \mathit{f} \mathit{g}
|
[math]\displaystyle{ \mathit{a} \mathit{b} \mathit{c} \mathit{d} \mathit{e} \mathit{f} \mathit{g} \,\! }[/math] |
\mathit{h} \mathit{i} \mathit{j} \mathit{k} \mathit{l} \mathit{m}
|
[math]\displaystyle{ \mathit{h} \mathit{i} \mathit{j} \mathit{k} \mathit{l} \mathit{m} \,\! }[/math] |
\mathit{n} \mathit{o} \mathit{p} \mathit{q} \mathit{r} \mathit{s} \mathit{t}
|
[math]\displaystyle{ \mathit{n} \mathit{o} \mathit{p} \mathit{q} \mathit{r} \mathit{s} \mathit{t} \,\! }[/math] |
\mathit{u} \mathit{v} \mathit{w} \mathit{x} \mathit{y} \mathit{z}
|
[math]\displaystyle{ \mathit{u} \mathit{v} \mathit{w} \mathit{x} \mathit{y} \mathit{z} \,\! }[/math] |
\mathit{0} \mathit{1} \mathit{2} \mathit{3} \mathit{4}
|
[math]\displaystyle{ \mathit{0} \mathit{1} \mathit{2} \mathit{3} \mathit{4} \,\! }[/math] |
\mathit{5} \mathit{6} \mathit{7} \mathit{8} \mathit{9}
|
[math]\displaystyle{ \mathit{5} \mathit{6} \mathit{7} \mathit{8} \mathit{9}\,\! }[/math] |
| Roman typeface | |
\mathrm{A} \mathrm{B} \mathrm{C} \mathrm{D} \mathrm{E} \mathrm{F} \mathrm{G}
|
[math]\displaystyle{ \mathrm{A} \mathrm{B} \mathrm{C} \mathrm{D} \mathrm{E} \mathrm{F} \mathrm{G} \,\! }[/math] |
\mathrm{H} \mathrm{I} \mathrm{J} \mathrm{K} \mathrm{L} \mathrm{M}
|
[math]\displaystyle{ \mathrm{H} \mathrm{I} \mathrm{J} \mathrm{K} \mathrm{L} \mathrm{M} \,\! }[/math] |
\mathrm{N} \mathrm{O} \mathrm{P} \mathrm{Q} \mathrm{R} \mathrm{S} \mathrm{T}
|
[math]\displaystyle{ \mathrm{N} \mathrm{O} \mathrm{P} \mathrm{Q} \mathrm{R} \mathrm{S} \mathrm{T} \,\! }[/math] |
\mathrm{U} \mathrm{V} \mathrm{W} \mathrm{X} \mathrm{Y} \mathrm{Z}
|
[math]\displaystyle{ \mathrm{U} \mathrm{V} \mathrm{W} \mathrm{X} \mathrm{Y} \mathrm{Z} \,\! }[/math] |
\mathrm{a} \mathrm{b} \mathrm{c} \mathrm{d} \mathrm{e} \mathrm{f} \mathrm{g}
|
[math]\displaystyle{ \mathrm{a} \mathrm{b} \mathrm{c} \mathrm{d} \mathrm{e} \mathrm{f} \mathrm{g}\,\! }[/math] |
\mathrm{h} \mathrm{i} \mathrm{j} \mathrm{k} \mathrm{l} \mathrm{m}
|
[math]\displaystyle{ \mathrm{h} \mathrm{i} \mathrm{j} \mathrm{k} \mathrm{l} \mathrm{m} \,\! }[/math] |
\mathrm{n} \mathrm{o} \mathrm{p} \mathrm{q} \mathrm{r} \mathrm{s} \mathrm{t}
|
[math]\displaystyle{ \mathrm{n} \mathrm{o} \mathrm{p} \mathrm{q} \mathrm{r} \mathrm{s} \mathrm{t} \,\! }[/math] |
\mathrm{u} \mathrm{v} \mathrm{w} \mathrm{x} \mathrm{y} \mathrm{z}
|
[math]\displaystyle{ \mathrm{u} \mathrm{v} \mathrm{w} \mathrm{x} \mathrm{y} \mathrm{z} \,\! }[/math] |
\mathrm{0} \mathrm{1} \mathrm{2} \mathrm{3} \mathrm{4}
|
[math]\displaystyle{ \mathrm{0} \mathrm{1} \mathrm{2} \mathrm{3} \mathrm{4} \,\! }[/math] |
\mathrm{5} \mathrm{6} \mathrm{7} \mathrm{8} \mathrm{9}
|
[math]\displaystyle{ \mathrm{5} \mathrm{6} \mathrm{7} \mathrm{8} \mathrm{9}\,\! }[/math] |
| Fraktur typeface | |
\mathfrak{A} \mathfrak{B} \mathfrak{C} \mathfrak{D} \mathfrak{E} \mathfrak{F} \mathfrak{G}
|
[math]\displaystyle{ \mathfrak{A} \mathfrak{B} \mathfrak{C} \mathfrak{D} \mathfrak{E} \mathfrak{F} \mathfrak{G} \,\! }[/math] |
\mathfrak{H} \mathfrak{I} \mathfrak{J} \mathfrak{K} \mathfrak{L} \mathfrak{M}
|
[math]\displaystyle{ \mathfrak{H} \mathfrak{I} \mathfrak{J} \mathfrak{K} \mathfrak{L} \mathfrak{M} \,\! }[/math] |
\mathfrak{N} \mathfrak{O} \mathfrak{P} \mathfrak{Q} \mathfrak{R} \mathfrak{S} \mathfrak{T}
|
[math]\displaystyle{ \mathfrak{N} \mathfrak{O} \mathfrak{P} \mathfrak{Q} \mathfrak{R} \mathfrak{S} \mathfrak{T} \,\! }[/math] |
\mathfrak{U} \mathfrak{V} \mathfrak{W} \mathfrak{X} \mathfrak{Y} \mathfrak{Z}
|
[math]\displaystyle{ \mathfrak{U} \mathfrak{V} \mathfrak{W} \mathfrak{X} \mathfrak{Y} \mathfrak{Z} \,\! }[/math] |
\mathfrak{a} \mathfrak{b} \mathfrak{c} \mathfrak{d} \mathfrak{e} \mathfrak{f} \mathfrak{g}
|
[math]\displaystyle{ \mathfrak{a} \mathfrak{b} \mathfrak{c} \mathfrak{d} \mathfrak{e} \mathfrak{f} \mathfrak{g} \,\! }[/math] |
\mathfrak{h} \mathfrak{i} \mathfrak{j} \mathfrak{k} \mathfrak{l} \mathfrak{m}
|
[math]\displaystyle{ \mathfrak{h} \mathfrak{i} \mathfrak{j} \mathfrak{k} \mathfrak{l} \mathfrak{m} \,\! }[/math] |
\mathfrak{n} \mathfrak{o} \mathfrak{p} \mathfrak{q} \mathfrak{r} \mathfrak{s} \mathfrak{t}
|
[math]\displaystyle{ \mathfrak{n} \mathfrak{o} \mathfrak{p} \mathfrak{q} \mathfrak{r} \mathfrak{s} \mathfrak{t} \,\! }[/math] |
\mathfrak{u} \mathfrak{v} \mathfrak{w} \mathfrak{x} \mathfrak{y} \mathfrak{z}
|
[math]\displaystyle{ \mathfrak{u} \mathfrak{v} \mathfrak{w} \mathfrak{x} \mathfrak{y} \mathfrak{z} \,\! }[/math] |
\mathfrak{0} \mathfrak{1} \mathfrak{2} \mathfrak{3} \mathfrak{4}
|
[math]\displaystyle{ \mathfrak{0} \mathfrak{1} \mathfrak{2} \mathfrak{3} \mathfrak{4} \,\! }[/math] |
\mathfrak{5} \mathfrak{6} \mathfrak{7} \mathfrak{8} \mathfrak{9}
|
[math]\displaystyle{ \mathfrak{5} \mathfrak{6} \mathfrak{7} \mathfrak{8} \mathfrak{9}\,\! }[/math] |
| Calligraphy/Script | |
\mathcal{A} \mathcal{B} \mathcal{C} \mathcal{D} \mathcal{E} \mathcal{F} \mathcal{G}
|
[math]\displaystyle{ \mathcal{A} \mathcal{B} \mathcal{C} \mathcal{D} \mathcal{E} \mathcal{F} \mathcal{G} \,\! }[/math] |
\mathcal{H} \mathcal{I} \mathcal{J} \mathcal{K} \mathcal{L} \mathcal{M}
|
[math]\displaystyle{ \mathcal{H} \mathcal{I} \mathcal{J} \mathcal{K} \mathcal{L} \mathcal{M} \,\! }[/math] |
\mathcal{N} \mathcal{O} \mathcal{P} \mathcal{Q} \mathcal{R} \mathcal{S} \mathcal{T}
|
[math]\displaystyle{ \mathcal{N} \mathcal{O} \mathcal{P} \mathcal{Q} \mathcal{R} \mathcal{S} \mathcal{T} \,\! }[/math] |
\mathcal{U} \mathcal{V} \mathcal{W} \mathcal{X} \mathcal{Y} \mathcal{Z}
|
[math]\displaystyle{ \mathcal{U} \mathcal{V} \mathcal{W} \mathcal{X} \mathcal{Y} \mathcal{Z}\,\! }[/math] |
| Hebrew | |
\aleph \beth \gimel \daleth
|
[math]\displaystyle{ \aleph \beth \gimel \daleth\,\! }[/math] |
| Feature | Syntax | How it looks rendered | |
|---|---|---|---|
| non-italicised characters | \mbox{abc} | [math]\displaystyle{ \mbox{abc} }[/math] | [math]\displaystyle{ \mbox{abc} \,\! }[/math] |
| mixed italics (bad) | \mbox{if} n \mbox{is even} | [math]\displaystyle{ \mbox{if} n \mbox{is even} }[/math] | [math]\displaystyle{ \mbox{if} n \mbox{is even} \,\! }[/math] |
| mixed italics (good) | \mbox{if }n\mbox{ is even} | [math]\displaystyle{ \mbox{if }n\mbox{ is even} }[/math] | [math]\displaystyle{ \mbox{if }n\mbox{ is even} \,\! }[/math] |
| mixed italics (more legible: ~ is a non-breaking space, while "\ " forces a space) | \mbox{if}~n\ \mbox{is even} | [math]\displaystyle{ \mbox{if}~n\ \mbox{is even} }[/math] | [math]\displaystyle{ \mbox{if}~n\ \mbox{is even} \,\! }[/math] |
Alternatives
Formulas in simple text
These can be produced with:
- the keyboard symbols,
- the symbols from the virtual keyboard (available by clicking on the
 button in edit mode)
button in edit mode) - any other Unicode symbols
- formatting commands like
<sub> </sub>(subscript),<sup> </sup>(superscript),'' ''(italic)
The major drawback is that in this way only one-line simple formulas can be produced; multiline formula, fractions, matrices, etc cannot be created using simple text. However, it can prove handy for really small formula or variables/constants/functions definitions, and for people who do not master TeX.
- Examples
| Source code (in edit mode) | Result (in read mode) |
|---|---|
x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> |
x2 + y2 = z2 |
''π<sub>A</sub>(x) = 1 - (μ<sub>A</sub>(x) + ν<sub>A</sub>(x))'' |
πA(x) = 1 - (μA(x) + νA(x)) |
A = ∑<sub>i=1</sub><sup>n</sup> a<sub>i</sub> |
A = ∑i=1n ai |
Formulas in uploaded images
- You may first want to read Help:Upload and Help:Images and files.
The major drawbacks of this approach are:
- Images are difficult to edit, and need external graphic editor for this sake.
- Images may scale down, but may not scale up well (unless in vector graphic format).
- Images files may be unnecessary large.
- Files can only be uploaded by registered users.
Comparison
Image
[[Image:Equation-gn-transition-angle-brackets-3.png]]
Wiki markup
Z5 = < {l7, m4}, {l8, m5}, M5, Λ(l7, m3) >
- where
|
|
Z<sub>5</sub> = < {l<sub>7</sub>, m<sub>4</sub>}, {l<sub>8</sub>, m<sub>5</sub>}, IM<sub>P</sub>, Λ(l<sub>7</sub>, m<sub>3</sub>) >
: where
{{index-matrix/start
|matrix-id = IM<sub>P</sub>
|columns = 2
|1 = l<sub>8</sub>
|2 = m<sub>5</sub>
}}
{{index-matrix/row-predic
|columns= 2
|row-id = l<sub>7</sub>
|1 = true
|2 = false
}}
{{index-matrix/row-predic
|columns= 2
|row-id = m<sub>4</sub>
|1 = W<sub>4,8</sub>
|2 = W<sub>4,5</sub>
}}
{{index-matrix/end}}
TeX
[math]\displaystyle{ Z_5 = \big\lt \{ l_7, m_4 \}, \{ l_8, m_5 \}, \begin{array}{c|c c} & l_8 & m_5 \\ \hline l_7 & true & false \\ m_4 & W_{4,8} & W_{4,5} \\ \end{array}, \land (l_7, m_3) \big\gt }[/math]
<math>
Z_5 = \big< \{ l_7, m_4 \}, \{ l_8, m_5 \},
\begin{array}{c|c c} & l_8 & m_5 \\
\hline
l_7 & true & false \\
m_4 & W_{4,8} & W_{4,5} \\
\end{array},
\land (l_7, m_3) \big>
</math>
See also
- Help:Formulas/Formulas in MS Word
- Help:Displaying a formula on Meta-Wikipedia
- Manual of Style (mathematics) on English Wikipedia
- Help:Contents for other help pages