Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Deadline for submissions: 10 May 2026.
Ifigenia:Lecture courses/Generalized nets/Quiz
- This page provides a simple quiz on generalized nets.
|
<quiz display=simple> { Кой от следните елементи в дефиницията на обобщеномрежов преход е формулиран некоректно? |
type="()"}
+ Множество на входно-изходните позиции [math]\displaystyle{ L }[/math] . |
Обобщената мрежа има множество на входните позиции и множество на изходните позиции; понятието "множество на входно-изходните позиции" е некоректно формулирано.
- Продължителност на активното състояние на прехода [math]\displaystyle{ t_2 }[/math] . - Условие на прехода [math]\displaystyle{ r }[/math] . - Обект, подобен на булев израз [math]\displaystyle{ \square }[/math] . { В таблицата по-долу отбележете кои компоненти в дефиницията на обобщената мрежа отразяват нейната (A) статика, (B) динамика, (C) хронология, (D) памет. |
type="()" } | Динамика B | Хронология C | Памет D ---+ Функция Х, задаваща характеристики на ядрата при постъпването им в мрежата. --+- Продължителност на функционирането на обобщената мрежа t*. +--- Функция θ1, задаваща следващия момент от време, когато даден преход ще се активира. -+-- Функция θK, задаваща момента от време, когато дадено ядро може да постъпи в мрежата. +--- Множество А от преходите в мрежата. +--- Функция c, задаваща капацитетите на позициите. { Кой от следните компоненти задължително участва в дефиницията на минималната редуцирана обобщена мрежа? |
type="()"}
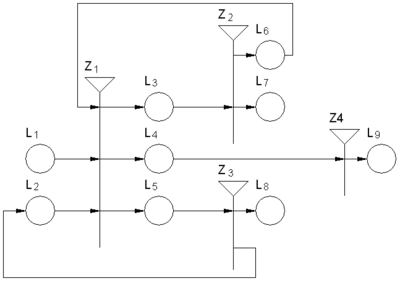
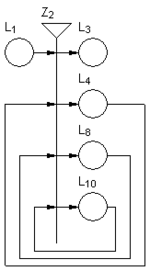
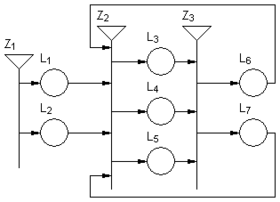
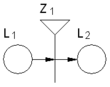
- Функция, изчисляваща вярностните стойности на предикатите в матрицата на преходите. - Функция, задаваща приоритетите на преходите. + Функция, задаваща началните характеристики на ядрата. - Продължителност на функционирането на модела. { Отбележете в коя от следните графични структури на обобщеномрежови модели има допусната грешка? |
type="()"} | Липсва входна позиция на мрежата.
{ Попълнете празното място с (една) подходяща дума, така че да се получи вярно твърдениe. |
type="{}"}
Елементите на индексираната матрица на { капацитетите _15 } могат да са естествените числа и безкрайност. Всяка цветна мрежа на Петри може да се представи чрез { редуцирана|цветна _15 } обобщена мрежа. Стратегиите за преминаване на ядра през преход се определят чрез { динамичен _15 } оператор. </quiz> |