Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Deadline for submissions: 10 May 2026.
IFSTool
IFSTool is a software for checking properties of intuitionistic fuzzy implications and negations. It is being developed by Dimitar Dimitrov in the frames of the bilateral scientific exchange project Design and development of intuitionistic fuzzy logic tools in information technologies. IFSTool requires Microsoft .NET Framework (already installed on newer MS Windows versions) to run.
Basic properties
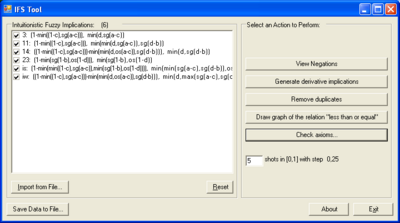
Some of the properties that can be checked are the following:
- Checking the validity of user-defined axioms of the classical and non-classical logics.
- Equivalence of implications and equivalence of negations.
- Order of implications and negations (generating the graph for the relation "less than or equal").
All generated data can be exported to various text and graphic formats, such as TeX, HTML, PNG and etc.
All implications (or negations, respectively) have to be imported by the user from external text files. Files should be in the following format:
- the definition of each implication/negation should be on a single line;
- no two definitions should share a single line;
- each line should begin with unique identifier of the implication/negation, followed by delimiter (": " or tab), then the first (validity) part of the implication/negation's definition, delimiter (", " or tab), and the second (nonvalidity) part of the implication/negation's definition;
- no spaces are allowed in the validity and nonvalidity parts;
- the left argument of the implications is <a, b> and the right one is <c, d>. For negations the argument is <a,b>. No other parameter names are allowed for now.
Here's a short example of a file which can be imported:
- 1: max(b,min(a,c)), min(a,d)
- 2: 1-sg(a-c), d*sg(a-c)
Checking the validity of user-defined axioms
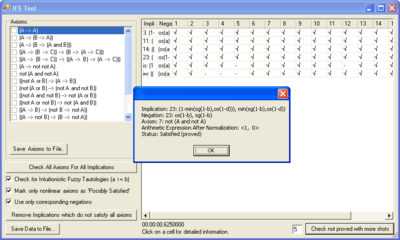
To check the validity of axioms for a set of implications (or negations), you have to execute the following steps:
- Click "Import from File" to load a text file with implications or negations. Several files can be imported and appended.
- Provide a text file named "Axioms.txt" in the directory where the IFSTool executable is located. The file should contain axioms in the following format:
- each axiom definition should be on a single line;
- no two definitions should share a single line;
- each line should begin with unique identifier of the axiom, followed by space, and then the definition of the axiom.
- IF variables should be named A, B, C, ..., Z. It is recommended to start with A, then B, and so on, otherwise the program will run significantly slower;
- IF constants can be set in the form <value1,value2>.
- The following operators can be used:
- \supset : the current implication that is tested;
- \neg : the corresponding negation of currently tested implication;
- \& : intuitionistic fuzzy conjunction (<a,b> \& <c,d> <=> min(a, c), max(b, d));
- \vee : intuitionistic fuzzy disjunction (<a,b> \vee <c,d> <=> max(a, c), min(b, d));
- \classicnot : the classical fuzzy negation (\classicnot <a,b> <=> <b,a>);
- = : equality (<a,b> = <c,d> <=> a=c and b=d);
- >= : greater-than-or-equal - (<a,b> >= <c,d> <=> a>=c and b<=d)
- <= : less-than-or-equal
- All operators should be surrounded with spaces.
- Example file:
- t0 A \supset A
- t14 A \supset (B \supset (A \& B))
- t21 (\neg A \vee B) \supset (A \supset B)
- ky3 (<0,1> \supset A) = <1,0>
- Set shots to 5.
- Click "Check axioms...". A new window is opened. The axioms should be visible on the left side of the window.
- There is an option "Check for Intuitionistic Fuzzy Tautologies". Deselect it if you want to check for non-intuitionistic tautologies (to check a expression if it is equal to <1,0>).
- Click "Check All Axioms For All Implications". This may take a lot of time, especially for relatively smaller steps (0.1 for example).
- A table with results is displayed. When clicking on a cell, the following information is displayed:
- the tested implication;
- the tested negation;
- the checked axiom;
- normalized arithmetic expression that corresponds to the axiom with the given implication and negation;
- the status of the axiom (for the given implication and negation) - one of the following: “Satisfied (proved)”, “Not satisfied (proved)” and “Possibly satisfied (No counterexample found)”.
- If there are possibly satisfied axioms, you can specify smaller step (larger number of shots) and then click "Check not proved with more shots". Some of the possibly satisfied axioms may turn to "Not satisfied (proved)". The rest should be proved manually (in next versions of the software this is going to be improved).
- By default, each axiom is tested with all implications and their corresponding negations. If "Use only corresponding negations" is unchecked, all axioms will be checked for all combinations of implications and negations.
Removal of duplicate operations
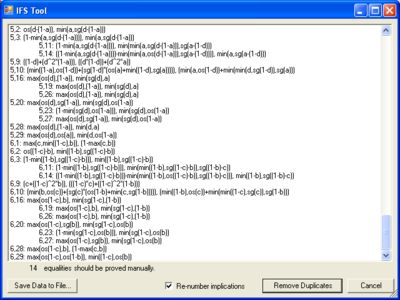
To remove duplicate implications (or negations, respectively):
- Import the implications/negations.
- Set shots = 5.
- Click "Remove duplicates". A detailed report is generated showing the groups of equivalent and possibly equivalent implications/negations.
- Check the lines marked with "(not proved)". If there are different implications/negations, marked as equivalent, go back to step 2 and specify bigger number.
- Click "Remove duplicates". There is an option for renumbering the implications/negations, since the initial numbering may not be continuous after removing some implications/negations.
To check if a new intuitionistic fuzzy implication (or negation, respectively) is not equivalent to some old one, the following approach can be used:
- Import all intuitionistic fuzzy implications/negations.
- Remove the duplicates, as described above.
- Import the new implication/negation and remove the duplicates again.
- If the new implication/negation is equivalent to some old one, this could be seen in the report window.
Drawing the graph of relations
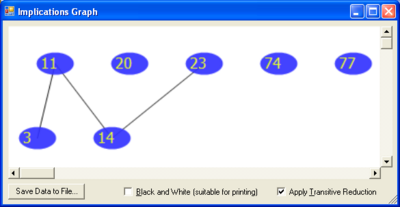
To draw a graph for the relation < :
- Import the implications or negations.
- Set shots to be 5 or more.
- Click “Draw graph for the relation “less than or equal””. This may take some time.
- By default, a transitive reduction is applied, since the relation < is transitive. If i1 < i2 and i2 < i3, the corresponding ribs are colored in black and the rib from i1 to i3 is colored in gray.
Algorithm
IFSTool uses binary trees to represent the expressions. When a formula has to be checked:
- The formula is optimized as much as possible. For example, a*(b-b) is equivalent to 0. Many IF-specific optimizations are performed.
- The formula is checked in several values. For example, if the step is 0.5 (3 shots in the interval [0, 1]), the following values are used: <0,0>, <0,0.5>, <0,1>, <0.5,0>, <0.5,0.5>, <1,0>. If the formula is not satisfied on any of the values, it is marked as “not satisfied” and no further checks are made for it.
- The formula is attempted to be proved by checking a large set of rules. For example, if max(x,y)>z has to be proved, it is replaced by the disjunction (x>z | y>z).