Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Deadline for submissions: 10 May 2026.
Generalized nets
Generalized nets (GNs) constitute a discrete tool for universal description of adaptable, flexible, structured and reusable models of complex systems with many different and interacting components, not necessarily of the homogeneous structure and origin, usually involved in parallel, simultaneous activities. Generalized nets represent a significant extension and generalization of the concept of Petri nets, as well as of other Petri nets extensions and modifications.
Components of a generalized net
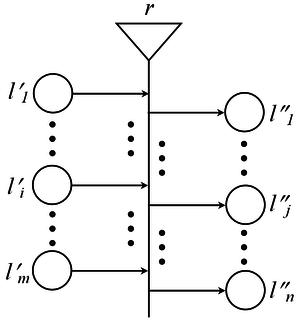
A generalized net consists of:
- a static structure,
- a dynamic structure,
- temporal components.
The static structure consists of objects called transitions, which have input and output places. Two transitions can share a place, but every place can be an input of at most one transition and can be an output of at most one transition.
The dynamic structure consists of tokens, which act as information carriers and can occupy a single place at every moment of the GN execution. The tokens pass through the transition from one input to another output place; such an ordered pair of places is called transition arc. The tokens' movement is governed by conditions (predicates), contained in the predicate matrix of the transition.
The information carried by a token is contained in its characteristics, which can be viewed as an associative array of characteristic names and values. The values of the token characteristics change in time according to specific rules, called characteristic functions. Every place possesses at most one characteristic function, which assigns new characteristics to the incoming tokens. Apart from movement in the net and change of the characteristics, tokens can also split and merge in the places.
The temporal components describe the time scale of GN execution. Temporal conditions control the transitions' moments of activation and duration of active state. Various other tools for fine tuning of the GN functioning are provided in the form of priorities of separate transitions, places and tokens, as well as capacities of places and transitions arcs.
Graphic representation
Formal description
Formally described, the generalized net is represented by the following four-tuple:
where:
- 1. Static structure
- [math]\displaystyle{ A }[/math] is a set of transitions (see the formal definition of a transition)
- [math]\displaystyle{ \pi_{A} }[/math] is a function giving the priorities of the transitions, i.e. [math]\displaystyle{ \pi_{A} : A \rightarrow N }[/math] where N = {0, 1, 2, ...} ∪ {∞}
- [math]\displaystyle{ \pi_{L} }[/math] is a function giving the priorities of the places, i.e. [math]\displaystyle{ \pi_{L} : L \rightarrow N }[/math]
- [math]\displaystyle{ c }[/math] is a function giving the place capacities, i.e. [math]\displaystyle{ c : L \rightarrow N }[/math]
- [math]\displaystyle{ f }[/math] is a function giving the truth value of the predicates. In the basic case, it may obtain values "true" (1) and "false" (0). In fuzzy generalized nets its domain is the [0;1] interval (see fuzzy set) and in the intuitionistic fuzzy generalized nets its domain is the set [0;1]×[0;1] (see intuitionistic fuzzy set).
- [math]\displaystyle{ \theta_{1} }[/math] is a function giving the next time moment when a given transition will be fired (will become active). Hence, [math]\displaystyle{ \theta_{1}(t) = t' }[/math] where [math]\displaystyle{ t, t' \in [T, T+t^*]; t \le t' }[/math]. The value of this function is being recalculated in the moment when the transition's active state ceases.
- [math]\displaystyle{ \theta_{2} }[/math] is a function giving the duration of the transition's active state. Hence, [math]\displaystyle{ \theta_{2}(t) = t' }[/math] where [math]\displaystyle{ t, t' \in [T, T+t^*]; t' \ge 0 }[/math]. The value of this function is calculated in the moment when the transition's active state begins.
- 2. Dynamic structure
- [math]\displaystyle{ K }[/math] is the set of tokens of the generalized net. In certain cases it is more convenient to denote this set as [math]\displaystyle{ K = \bigcup_{l \in Q^I} K_{l} }[/math] where [math]\displaystyle{ K_{l} }[/math] is the set of all GN tokens which are waiting to enter place [math]\displaystyle{ l }[/math] and [math]\displaystyle{ Q^I }[/math] is the set of all input places in the net.
- [math]\displaystyle{ \pi_K }[/math] is a function giving the priorities of the tokens, i.e. [math]\displaystyle{ \pi_{K} : K \rightarrow N }[/math]
- [math]\displaystyle{ \theta_K }[/math] is a function giving the moment of time when a given token may enter the GN, i.e. [math]\displaystyle{ \theta_K (\alpha)=t }[/math] where [math]\displaystyle{ \alpha \in K, t \in [T; T+t^*] }[/math]
- 3. Time
- [math]\displaystyle{ T }[/math] is the moment of time when the generalized net starts functioning. This moment is determined according to a fixed global timescale.
- [math]\displaystyle{ t^0 }[/math] is the elementary time step of the fixed global timescale (the interval with which time increments in the timescale).
- [math]\displaystyle{ t^* }[/math] is the total duration of functioning of the net.
- 4. Memory
- [math]\displaystyle{ X }[/math] is the set of initial characteristics, which tokens may exhibit when they enter the net for first.
- [math]\displaystyle{ \Phi }[/math] is a characteristic function, which assigns a new characteristic to each token when it makes the transfer from an input to an output place of a given transition.
- [math]\displaystyle{ b }[/math] is a function giving the maximal number of characteristics, which a given token may obtain during its movement throughout the net, i.e. [math]\displaystyle{ b : K \rightarrow N }[/math]. In general, [math]\displaystyle{ b }[/math] may possess four different values: 0, 1, [math]\displaystyle{ s }[/math] or [math]\displaystyle{ \infty }[/math] meaning that the token keeps, respectively: none of its characteristics, its last characteristic, its last [math]\displaystyle{ s }[/math] characteristics, or all of its characteristics obtained during its movement in the net.
In a Petri net implementation, parallelism is reduced to a sequential firing of the net transitions and in general the order of their activation is probabilistic or dependent on the transitions' priorities, if any. The respective algorithms for generalized nets enable a more detailed modelling of the described process.
In the the book "Generalized Nets" from 1991 year [1], there were formulated two major algorithms, related to generalized nets:
- Algorithm for transition functioning, which is to some extent equivalent to the tokens transfer algorithm in Petri nets, and
- Algorithm for generalized net functioning.
The algorithm for transition functioning was later modified in 2007 [2].
Theorem 20 in the book "On Generalized Nets Theory" from 2007 year [3] states that the functioning and the results of the work of a given GN transition are equal for both algorithms, yet the difference between both algorithms is that in almost any case the modified algorithm yields results more quickly.
Reduced generalized nets
Extensions of generalized nets
Generalized nets have been subject of multiple different extensions. For each of these it has been proved that represents a conservative extension, i.e. there exists an ordinary generalized net which describes the extended GN, i.e. both nets have the same modelling capabilities.
The following extensions of GNs have been determined so far:
- Intuitionistic fuzzy generalized nets of type 1
- Intuitionistic fuzzy generalized nets of type 2
- Intuitionistic fuzzy generalized nets of type 3
- Intuitionistic fuzzy generalized nets of type 4
- Colour generalized nets
- Generalized nets with interval activation time
- Generalized nets with complex structure
- Generalized nets with global memory
- Generalized nets with optimization components
- Generalized nets with additional clocks
- Opposite generalized nets
- Generalized nets with three-dimensional structure
Theoretical aspects of generalized nets
Algebraic aspect
Topological aspect
Logical aspect
Functional aspect
- Global operators
- Local operators
- Hierarchical operators
- Reducing operators
- Extending operators
- Dynamic operators
Construction of generalized nets
Modelling and simulation
Software implementation of generalized nets
See also
- Theory of generalized nets
- Applications of generalized nets
- History of generalized nets
- List of GN terms
References
- ↑ Atanassov K., "Generalized Nets", World Scientific, Singapore, 1991, ISBN 978-981-02-0598-0
- ↑ Atanassov K., Tasseva V., Trifonov T., [[Issue:Modification of the algorithm for token transfer in generalized nets|]], Cybernetics and Information Technologies, Vol. 7, 2007, Np. 1, 62-66
- ↑ Atanassov K., On Generalized Nets Theory, "Professor Marin Drinov" Academic Publishing House, 2007, ISBN 978-954-322-237-7