Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Project:DMEU/Обобщени мрежи
Изследване на възможностите
за използване на Data Mining за управление на процеси в електронен университет
Data Mining in Electronic University
(DMEU) |
Обобщените мрежи, ОМ (Generalized nets, GNs) са средство за конструиране на адаптивни, гъвкави и структурирани модели на комплексни системи, в които протичат паралелни във времето процеси и са изградени от множество взаимодействащи си компоненти. Обобщените мрежи представляват значително разширение и обобщение на понятието мрежи на Петри, както и на други разширения и модификации на мрежи на Петри.
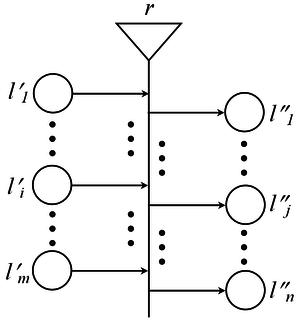
Обобщената мрежа е изградена от преходи (transitions). Преходът в контекста на обобщените мрежи е обект от статичната структура на мрежата, който съдържа условията за преминаването на ядра (token) от входните в изходните му позиции (places), след като преходът се е активирал.
От позиция или в позиция на прехода може да излиза или съответно да влиза не повече от една дъга. Позиция, от която излиза дъга се нарича входна за прехода, а позиция, в която влиза дъга се нарича изходна за прехода. Всеки преход в ОМ има поне една входна и поне една изходна позиция. Входна позиция, в която не влиза дъга се нарича вход на мрежата, а изходна позиция, от която не излиза дъга – изход на мрежата. В позициите може да има ядра. Те се преместват от входните към съответните изходни позиции на преходите. Когато настъпи определения за прехода момент от време, и във входните позиции има достатъчен брой ядра, то ядрата от входните позиции придобиват възможност да се придвижат до изходните позиции. Този процес се нарича активиране на прехода. В началото ядрата, които постъпват в мрежата през входните й позиции имат т.нар. начални характеристики. При всяко преминаване през преход в мрежата те получават нови характеристики и така всяко ядро в мрежата е уникално и има своя история. Всяка позиция има свой капацитет.
Формално описание на преход
Преходът Z в ОМ се представя като наредена последователност от седем компоненти:
където:
- [math]\displaystyle{ L' }[/math] са крайно непразно множество от входните позиции на прехода.
- [math]\displaystyle{ L'' }[/math] са крайно непразно множество от изходните позиции на прехода.
- [math]\displaystyle{ t_1 }[/math] е момент време на активиране на прехода.
- [math]\displaystyle{ t_2 }[/math] задава продължителността на активното състояние на прехода.
- [math]\displaystyle{ r }[/math] е условие на прехода. Представлява индексирана матрица от вида:
- [math]\displaystyle{ r = \begin{array}{c|c c c c c} & l''_1 & ... & l''_j & ... & l''_n \\ \hline l'_1 & & & & & \\ ... & & & & & \\ l'_i & & & r_{i,j} & & \\ ... & & & & & \\ l'_m & & & & & \\ \end{array} }[/math]
- където [math]\displaystyle{ r_{i,j} }[/math] са предикати, [math]\displaystyle{ 1 \le i \le m, 1 \le j \le n }[/math]
- [math]\displaystyle{ M }[/math] задава капацитетите на дъгите. Представлява индексирана матрица от вида:
- [math]\displaystyle{ M = \begin{array}{c|c c c c c} & l''_1 & ... & l''_j & ... & l''_n \\ \hline l'_1 & & & & & \\ ... & & & & & \\ l'_i & & & M_{i,j} & & \\ ... & & & & & \\ l'_m & & & & & \\ \end{array} }[/math]
- където [math]\displaystyle{ M_{i,j} \ge 0 }[/math] са естествени числа и [math]\displaystyle{ \infty }[/math], [math]\displaystyle{ 1 \le i \le m, 1 \le j \le n }[/math]
- [math]\displaystyle{ \Box }[/math] се нарича тип на прехода и представлява булев израз. Ако стойността му е “true” съответният преход може да се активира, а ако е “false” - не. В него участват идентификаторите на всички входни позиции на прехода, свързани с логическите операции "и" [math]\displaystyle{ \land }[/math] и "или" [math]\displaystyle{ \lor }[/math]:
- [math]\displaystyle{ \land(l_{i_1}, l_{i_2},...,l_{i_u}) }[/math] - във всяка входна позиция [math]\displaystyle{ l_{i_1}, l_{i_2},...,l_{i_u} }[/math] трябва да има най-малко по едно ядро,
- [math]\displaystyle{ \lor(l_{i_1}, l_{i_2},...,l_{i_u}) }[/math] - най-малко в една от входните позиции [math]\displaystyle{ l_{i_1}, l_{i_2},...,l_{i_u} }[/math] трябва да има най-малко едно ядро.
Формално описание на Обобщена мрежа
Обобщена мрежа е наредената четворка:
където:
- 1. Статична структура (Static structure)
- [math]\displaystyle{ A }[/math] е множеството от всички преходи в мрежата.
- [math]\displaystyle{ \pi_{A} }[/math] е функция, задаваща приоритетите на преходите, т.е. [math]\displaystyle{ \pi_{A} : A \rightarrow N }[/math] където N = {0, 1, 2, ...} ∪ {∞}.
- [math]\displaystyle{ \pi_{L} }[/math] е функция, задаваща приоритетите на позициите, т.е. [math]\displaystyle{ \pi_{L} : L \rightarrow N }[/math].
- [math]\displaystyle{ c }[/math] е функция, задаваща капацитетите на позициите, т.е. [math]\displaystyle{ c : L \rightarrow N }[/math].
- [math]\displaystyle{ f }[/math] е функция, определяща вярностната стойност на предикатите.
- [math]\displaystyle{ \theta_{1} }[/math] задава следващия момент, в който може да се активира прехода. Стойността на тази функция се преизчислява в момента, в който завършва активното състояние на прехода. Оттук [math]\displaystyle{ \theta_{1}(t) = t' }[/math] където [math]\displaystyle{ t, t' \in [T, T+t^*]; t \le t' }[/math]
- [math]\displaystyle{ \theta_{2} }[/math] е функция, която задава продължителността на активното състояние на даден преход. Стойността й се изчислява в момента, в който се активира прехода. Оттук [math]\displaystyle{ \theta_{2}(t) = t' }[/math] където [math]\displaystyle{ t, t' \in [T, T+t^*]; t' \ge 0 }[/math].
- 2. Динамична структура (Dynamic structure)
- [math]\displaystyle{ K }[/math] е множество от ядрата в обобщената мрежа.
- [math]\displaystyle{ \pi_K }[/math] е функция, която задава приоритетите на ядрата, т.е. [math]\displaystyle{ \pi_{K} : K \rightarrow N }[/math]
- [math]\displaystyle{ \theta_K }[/math] е функция, която задава момента от време, в който определено ядро може да влезе в ОМ, т.е. [math]\displaystyle{ \theta_K (\alpha)=t }[/math] където [math]\displaystyle{ \alpha \in K, t \in [T; T+t^*] }[/math]
- 3. Времева компонента (Time)
- [math]\displaystyle{ T }[/math] е начален момент от време, в който ОМ започва функционирането си. Моментът Т се определя по фиксирана времева скала.
- [math]\displaystyle{ t^0 }[/math] е времева стъпка на фиксирана времева скала.
- [math]\displaystyle{ t^* }[/math] продължителност на функционирането на ОМ.
- 4. Компонента памет (Memory)
- [math]\displaystyle{ X }[/math] е множество на началните характеристики, с които ядрата влизат в мрежата.
- [math]\displaystyle{ \Phi }[/math] е характеристична функция. Тя определя новата характеристика на ядрото при преместването му от входната позиция на даден преход в изходната.
- [math]\displaystyle{ b }[/math] е функция, задаваща максималния брой характеристики, които едно ядро може да получи по време на движението си в ОМ, т.e. [math]\displaystyle{ b : K \rightarrow N }[/math].
References
- On Generalized Nets Theory, Krassimir Atanassov, Prof. Marin Drinov Academic Publishing House, Sofia, 2007