Generalized nets

Generalized nets (GNs) constitute a discrete tool for universal description of adaptable, flexible, structured and reusable models of complex systems with many different and interacting components, not necessarily of the homogeneous structure and origin, usually involved in parallel, simultaneous activities. Generalized nets represent a significant extension and generalization of the concept of Petri nets, as well as of other Petri nets extensions and modifications.

Components of a generalized net

A GN transition with m inputs and n outputs

A generalized net consists of:

• a static structure,
• a dynamic structure,
• temporal components.

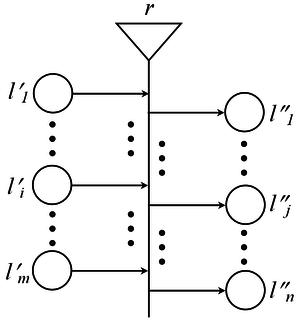
The static structure consists of objects called transitions, which have input and output places. Two transitions can share a place, but every place can be an input of at most one transition and can be an output of at most one transition.

The dynamic structure consists of tokens, which act as information carriers and can occupy a single place at every moment of the GN execution. The tokens pass through the transition from one input to another output place; such an ordered pair of places is called transition arc. The tokens' movement is governed by conditions (predicates), contained in the predicate matrix of the transition.

The information carried by a token is contained in its characteristics, which can be viewed as an associative array of characteristic names and values. The values of the token characteristics change in time according to specific rules, called characteristic functions. Every place possesses at most one characteristic function, which assigns new characteristics to the incoming tokens. Apart from movement in the net and change of the characteristics, tokens can also split and merge in the places.

The temporal components describe the time scale of GN execution. Temporal conditions control the transitions' moments of activation and duration of active state. Various other tools for fine tuning of the GN functioning are provided in the form of priorities of separate transitions, places and tokens, as well as capacities of places and transitions arcs.

Theoretical aspects of generalized nets

Functional aspect

• Global operators
• Local operators
• Hierarchical operators
• Reducing operators
• Extending operators
• Dynamic operators

See also

• Theory of generalized nets
• Applications of generalized nets
• History of generalized nets
• List of GN terms

References

This article is a stub. You can help Ifigenia by expanding it.