Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Deadline for submissions: 10 May 2026.
Necessity and possibility
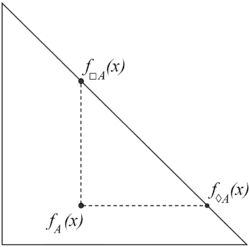
Necessity and possibility in the context of intuitionistic fuzzy sets are two modal operators defined as follows:
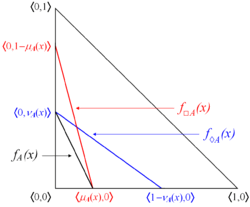
Let [math]\displaystyle{ E }[/math] be a fixed universe and [math]\displaystyle{ A \subset E }[/math] be a given set. Let functions [math]\displaystyle{ \mu_A, \nu_A \ : \ E \ \rightarrow [0,1] }[/math] determine the degrees of membership and non-membership. Then, the sets
[math]\displaystyle{ \Box A = \lbrace \langle x, \mu_A(x), 1 - \mu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]
[math]\displaystyle{ \Diamond A = \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]
are called, respectively, necessity and possibility operators.
When [math]\displaystyle{ A }[/math] is a proper IFS, i.e. there exists an element [math]\displaystyle{ x \in E }[/math] for which [math]\displaystyle{ \mu_A(x) \gt 0 }[/math], then
[math]\displaystyle{ \Box A \subset A \subset \Diamond A }[/math]
[math]\displaystyle{ \Box A \ne A \ne \Diamond A }[/math].
Obviously, for every fuzzy set, i.e. intuitionistic fuzzy set with [math]\displaystyle{ (\forall x \in E)(\pi_A(x) = 0) }[/math] it holds that
[math]\displaystyle{ \Box A = A = \Diamond A }[/math].
These operators are meaningless in the case of fuzzy sets, hence, this is a demonstration that intuitionistic fuzzy sets are proper extensions of the ordinary fuzzy sets. Both operators were defined in May 1983 by Krassimir Atanassov.
Propositions about necessity and possibility
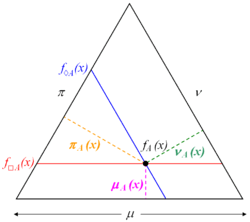
For every intuitionistic fuzzy set the following statements are valid:[1]
Proof of the first statement:
The following statements are also valid:[2]
Proof of the first statement:
References
- ↑ Proposition 1.42, page 61 from Intuitionistic Fuzzy Sets: Theory and Applications, Krassimir Atanassov, Springer, 1999.
- ↑ Theorem 1.43, page 62 from Intuitionistic Fuzzy Sets: Theory and Applications, Krassimir Atanassov, Springer, 1999.