Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Deadline for submissions: 10 May 2026.
Closure and interior
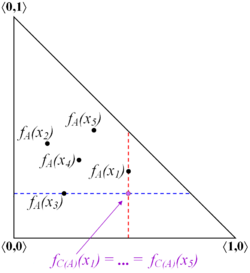
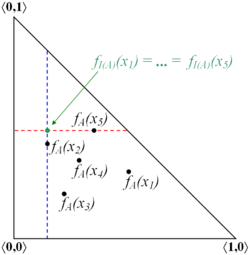
Closure and interior are two topological operators, defined over intuitionistic fuzzy sets, as follows.
Let [math]\displaystyle{ A \subset E }[/math] be an IFS. Then,
[math]\displaystyle{ C(A) = \lbrace \langle x, \sup_{y \in E} \mu_A(y), \inf_{y \in E} \nu_A(y) \rangle \ | \ x \in E \rbrace }[/math]
[math]\displaystyle{ I(A) = \lbrace \langle x, \inf_{y \in E} \mu_A(y), \sup_{y \in E} \nu_A(y) \rangle \ | \ x \in E \rbrace }[/math]
are respectively called closure and interior.
The following basic statements are valid:
- [math]\displaystyle{ C(A) }[/math] and [math]\displaystyle{ I(A) }[/math] are intuitionistic fuzzy sets.
- [math]\displaystyle{ I(A) \subset A \subset C(A) }[/math]
- [math]\displaystyle{ C(C(A)) \ = \ C(A) }[/math]
- [math]\displaystyle{ C(I(A)) \ = \ I(A) }[/math]
- [math]\displaystyle{ I(C(A)) \ = \ C(A) }[/math]
- [math]\displaystyle{ I(I(A)) \ = \ I(A) }[/math]
When operations and relations are applied over the closure and interior operators, the following valid statements can be formulated:
- [math]\displaystyle{ C(A \cap B) \ = \ C(A) \cap C(B) }[/math]
- [math]\displaystyle{ C(A \cup B) \ \subset \ C(A) \cup C(B) }[/math]
- [math]\displaystyle{ I(A \cap B) \ \supset \ I(A) \cap I(B) }[/math]
- [math]\displaystyle{ I(A \cup B) \ = \ I(A) \cup I(B) }[/math]
- [math]\displaystyle{ \overline{I(\overline{A})} \ = \ C(A) }[/math]
Further, when the modal operators necessity and possibility are applied, it holds that:
- [math]\displaystyle{ \Box (C(A)) \ = \ C(\Box(A)) }[/math]
- [math]\displaystyle{ \Box (I(A)) \ = \ I(\Box(A)) }[/math]
- [math]\displaystyle{ \Diamond (C(A)) \ = \ C(\Diamond (A)) }[/math]
- [math]\displaystyle{ \Diamond (I(A)) \ = \ I(\Diamond (A)) }[/math]
If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are intuitionistic fuzzy sets over [math]\displaystyle{ E }[/math], the following statements hold about them:
- If [math]\displaystyle{ A \subset B }[/math], then [math]\displaystyle{ I(A) \subset I(B) }[/math] and [math]\displaystyle{ C(A) \subset C(B) }[/math].