Necessity and possibility

Geometrical interpretation of necessity and possibility with a point

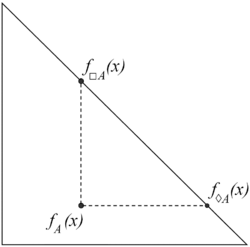
Necessity and possibility in the context of intuitionistic fuzzy sets are two modal operators defined as follows:

Let [math]\displaystyle{ E }[/math] be a fixed universe and [math]\displaystyle{ A \subset E }[/math] be a given set. Let functions [math]\displaystyle{ \mu_A, \nu_A \ : \ E \ \rightarrow [0,1] }[/math] determine the degrees of membership and non-membership. Then, the sets

[math]\displaystyle{ \Box A = \lbrace \langle x, \mu_A(x), 1 - \mu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]

[math]\displaystyle{ \Diamond A = \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]

are called, respectively, necessity and possibility operators.

When [math]\displaystyle{ A }[/math] is a proper IFS, i.e. there exists an element [math]\displaystyle{ x \in E }[/math] for which [math]\displaystyle{ \mu_A(x) \gt 0 }[/math], then

[math]\displaystyle{ \Box A \subset A \subset \Diamond A }[/math]

[math]\displaystyle{ \Box A \ne A \ne \Diamond A }[/math].

Obviously, for every fuzzy set, i.e. intuitionistic fuzzy set with [math]\displaystyle{ (\forall x \in E)(\pi_A(x) = 0) }[/math] it holds that

[math]\displaystyle{ \Box A = A = \Diamond A }[/math].

Propositions about necessity and possibility

A possible, though rarely used, geometrical interpretation of necessity and possibility with segments

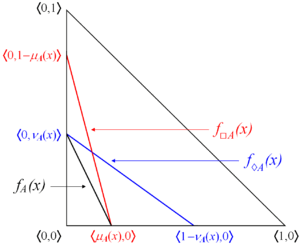
For every intuitionistic fuzzy set the following statements are valid:

[math]\displaystyle{ \begin{array}{r c l} & \\ \overline{\Box \overline{A}} & = & \Diamond A \\ \overline{\Diamond \overline{A}} & = & \Box A \\ \Box \Box A & = & \Box A \\ \Box \Diamond A & = & \Diamond A \\ \Diamond \Box A & = & \Box A \\ \Diamond \Diamond A & = & \Diamond A \end{array} }[/math]

Proof of the first statement:

[math]\displaystyle{ \begin{array}{r l} & \\ \overline{\Box \overline{A}} \ = & \overline{\Box \lbrace \langle x, \nu_A(x), \mu_A(x) \rbrace \ | \ x \in E \rbrace} \\ = & \overline{\lbrace \langle x, \nu_A(x), 1 - \nu_A(x) \rbrace \ | \ x \in E \rbrace} \\ = & \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace \\ = & \Diamond A \end{array} }[/math]

The following statements are also valid:

[math]\displaystyle{ \begin{array}{r c l} & \\ \Box (A \cap B) & = & \Box A \cap \Box B \\ \Box (A \cup B) & = & \Box A \cup \Box B \\ \overline{\Box (\overline{A} + \overline{B})} & = & \Diamond A . \Diamond B \\ \overline{\Box (\overline{A} . \overline{B})} & = & \Diamond A + \Diamond B \\ \Diamond (A \cap B) & = & \Diamond A \cap \Diamond B \\ \Diamond (A \cup B) & = & \Diamond A \cup \Diamond B \\ \overline{\Diamond (\overline{A} + \overline{B})} & = & \Box A . \Box B \\ \overline{\Diamond (\overline{A} . \overline{B})} & = & \Box A + \Box B \\ \end{array} }[/math]