Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Necessity and possibility: Difference between revisions
New page: '''Necessity and possibility''' in the context of intuitionistic fuzzy sets are two modal operators defined as follows: Let <math>E</math>... |
No edit summary |
||
| Line 1: | Line 1: | ||
[[Image:IFS-necessity-possibility.gif|right|thumb|250px|[[Geometrical interpretations of intuitionistic fuzzy sets|Geometrical interpretation]] of necessity and possibility ]] | |||
'''Necessity and possibility''' in the context of [[intuitionistic fuzzy sets]] are two modal [[Operators over intuitionistic fuzzy sets|operators]] defined as follows: | '''Necessity and possibility''' in the context of [[intuitionistic fuzzy sets]] are two modal [[Operators over intuitionistic fuzzy sets|operators]] defined as follows: | ||
| Line 19: | Line 20: | ||
</div> | </div> | ||
Obviously, for every [[fuzzy set]], i.e. intuitionistic fuzzy set with <math>(\forall x \in E)(\pi_A(x) = 0)</math> it holds that | |||
<div align="center"> | <div align="center"> | ||
| Line 25: | Line 26: | ||
</div> | </div> | ||
[[Category: | == Propositions about necessity and possibility == | ||
For every intuitionistic fuzzy set the following statements are valid:<ref>Proposition 1.42, page 61 from [[Intuitionistic Fuzzy Sets: Theory and Applications]], [[Krassimir Atanassov]], Springer, 1999.</ref> | |||
<div align="center"><math> | |||
\begin{array}{r c l} & \\ | |||
\overline{\Box \overline{A}} & = & \Diamond A \\ | |||
\overline{\Diamond \overline{A}} & = & \Box A \\ | |||
\Box \Box A & = & \Box A \\ | |||
\Box \Diamond A & = & \Diamond A \\ | |||
\Diamond \Box A & = & \Box A \\ | |||
\Diamond \Diamond A & = & \Diamond A | |||
\end{array} | |||
</math></div> | |||
''Proof of the first statement:'' | |||
<div align="center"><math> | |||
\begin{array}{r l} & \\ | |||
\overline{\Box \overline{A}} \ = & \overline{\Box \lbrace \langle x, \nu_A(x), \mu_A(x) \rbrace \ | \ x \in E \rbrace} \\ | |||
= & \overline{\lbrace \langle x, \nu_A(x), 1 - \nu_A(x) \rbrace \ | \ x \in E \rbrace} \\ | |||
= & \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace \\ | |||
= & \Diamond A | |||
\end{array} | |||
</math></div> | |||
The following statements are also valid:<ref>Theorem 1.43, page 62 from [[Intuitionistic Fuzzy Sets: Theory and Applications]], [[Krassimir Atanassov]], Springer, 1999.</ref> | |||
<div align="center"><math> | |||
\begin{array}{r c l} & \\ | |||
\Box (A \cap B) & = & \Box A \cap \Box B \\ | |||
\Box (A \cup B) & = & \Box A \cup \Box B \\ | |||
\overline{\Box (\overline{A} + \overline{B})} & = & \Diamond A . \Diamond B \\ | |||
\overline{\Box (\overline{A} . \overline{B})} & = & \Diamond A + \Diamond B \\ | |||
\Diamond (A \cap B) & = & \Diamond A \cap \Diamond B \\ | |||
\Diamond (A \cup B) & = & \Diamond A \cup \Diamond B \\ | |||
\overline{\Diamond (\overline{A} + \overline{B})} & = & \Box A . \Box B \\ | |||
\overline{\Diamond (\overline{A} . \overline{B})} & = & \Box A + \Box B \\ | |||
\end{array} | |||
</math></div> | |||
== References == | |||
<references /> | |||
[[Category:Intuitionistic fuzzy sets]] | |||
Revision as of 18:29, 13 April 2009
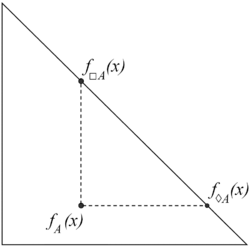
Necessity and possibility in the context of intuitionistic fuzzy sets are two modal operators defined as follows:
Let [math]\displaystyle{ E }[/math] be a fixed universe and [math]\displaystyle{ A \subset E }[/math] be a given set. Let functions [math]\displaystyle{ \mu_A, \nu_A \ : \ E \ \rightarrow [0,1] }[/math] determine the degrees of membership and non-membership. Then,
[math]\displaystyle{ \Box A = \lbrace \langle x, \mu_A(x), 1 - \mu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]
[math]\displaystyle{ \Diamond A = \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]
are called, respectively, necessity and possibility.
When [math]\displaystyle{ A }[/math] is a proper IFS, i.e. there exists an element [math]\displaystyle{ x \in E }[/math] for which [math]\displaystyle{ \mu_A(x) \gt 0 }[/math], then
[math]\displaystyle{ \Box A \subset A \subset \Diamond A }[/math]
[math]\displaystyle{ \Box A \ne A \ne \Diamond A }[/math].
Obviously, for every fuzzy set, i.e. intuitionistic fuzzy set with [math]\displaystyle{ (\forall x \in E)(\pi_A(x) = 0) }[/math] it holds that
[math]\displaystyle{ \Box A = A = \Diamond A }[/math].
Propositions about necessity and possibility
For every intuitionistic fuzzy set the following statements are valid:[1]
Proof of the first statement:
The following statements are also valid:[2]
References
- ↑ Proposition 1.42, page 61 from Intuitionistic Fuzzy Sets: Theory and Applications, Krassimir Atanassov, Springer, 1999.
- ↑ Theorem 1.43, page 62 from Intuitionistic Fuzzy Sets: Theory and Applications, Krassimir Atanassov, Springer, 1999.