Please check our Instructions to Authors and send your manuscripts to nifs.journal@gmail.com.
Necessity and possibility: Difference between revisions
New page: '''Necessity and possibility''' in the context of intuitionistic fuzzy sets are two modal operators defined as follows: Let <math>E</math>... |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Image:IFS-necessity-possibility.gif|right|thumb|250px|The most common [[Geometrical interpretations of intuitionistic fuzzy sets|geometrical interpretation]] of necessity and possibility with a point]] | |||
'''Necessity and possibility''' in the context of [[intuitionistic fuzzy sets]] are two modal [[Operators over intuitionistic fuzzy sets|operators]] defined as follows: | '''Necessity and possibility''' in the context of [[intuitionistic fuzzy sets]] are two modal [[Operators over intuitionistic fuzzy sets|operators]] defined as follows: | ||
Let <math>E</math> be a fixed universe and <math>A \subset E</math> be a given set. Let functions <math>\mu_A, \nu_A \ : \ E \ \rightarrow [0,1]</math> determine the degrees of [[membership]] and [[non-membership]]. Then, | Let <math>E</math> be a fixed universe and <math>A \subset E</math> be a given set. Let functions <math>\mu_A, \nu_A \ : \ E \ \rightarrow [0,1]</math> determine the degrees of [[membership]] and [[non-membership]]. Then, the sets | ||
<div align="center"> | <div align="center"> | ||
| Line 9: | Line 10: | ||
</div> | </div> | ||
are called, respectively, necessity and possibility. | are called, respectively, necessity and possibility operators. | ||
When <math>A</math> is a proper IFS, i.e. there exists an element <math>x \in E</math> for which <math>\mu_A(x) > 0</math>, then | When <math>A</math> is a proper IFS, i.e. there exists an element <math>x \in E</math> for which <math>\mu_A(x) > 0</math>, then | ||
| Line 19: | Line 20: | ||
</div> | </div> | ||
Obviously, for every [[fuzzy set]], i.e. intuitionistic fuzzy set with <math>(\forall x \in E)(\pi_A(x) = 0)</math> it holds that | |||
<div align="center"> | <div align="center"> | ||
| Line 25: | Line 26: | ||
</div> | </div> | ||
[[Category: | These operators are meaningless in the case of fuzzy sets, hence, this is a demonstration that intuitionistic fuzzy sets are proper extensions of the ordinary fuzzy sets. Both operators were defined in May 1983 by [[Krassimir Atanassov]]. | ||
== Propositions about necessity and possibility == | |||
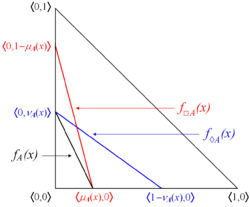
[[Image:IFS-necessity-possibility-with-segments.gif|right|thumb|250px|A possible, though rarely used, geometrical interpretation of necessity and possibility with segments]] | |||
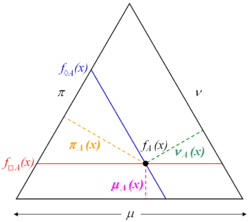
[[Image:IFS-necessity-possibility-equilateral-triangle.gif|right|thumb|250px|Another possible geometrical interpretation, within the equilateral triangle]] | |||
For every intuitionistic fuzzy set the following statements are valid:<ref>Proposition 1.42, page 61 from [[Intuitionistic Fuzzy Sets: Theory and Applications]], [[Krassimir Atanassov]], Springer, 1999.</ref> | |||
<div align="center"><math> | |||
\begin{array}{r c l} & \\ | |||
\overline{\Box \overline{A}} & = & \Diamond A \\ | |||
\overline{\Diamond \overline{A}} & = & \Box A \\ | |||
\Box \Box A & = & \Box A \\ | |||
\Box \Diamond A & = & \Diamond A \\ | |||
\Diamond \Box A & = & \Box A \\ | |||
\Diamond \Diamond A & = & \Diamond A | |||
\end{array} | |||
</math></div> | |||
''Proof of the first statement:'' | |||
<div align="center"><math> | |||
\begin{array}{r l} & \\ | |||
\overline{\Box \overline{A}} \ = & \overline{\Box \lbrace \langle x, \nu_A(x), \mu_A(x) \rbrace \ | \ x \in E \rbrace} \\ | |||
= & \overline{\lbrace \langle x, \nu_A(x), 1 - \nu_A(x) \rbrace \ | \ x \in E \rbrace} \\ | |||
= & \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace \\ | |||
= & \Diamond A | |||
\end{array} | |||
</math></div> | |||
The following statements are also valid:<ref>Theorem 1.43, page 62 from [[Intuitionistic Fuzzy Sets: Theory and Applications]], [[Krassimir Atanassov]], Springer, 1999.</ref> | |||
<div align="center"><math> | |||
\begin{array}{r c l} & \\ | |||
\Box (A \cap B) & = & \Box A \cap \Box B \\ | |||
\Box (A \cup B) & = & \Box A \cup \Box B \\ | |||
\overline{\Box (\overline{A} + \overline{B})} & = & \Diamond A . \Diamond B \\ | |||
\overline{\Box (\overline{A} . \overline{B})} & = & \Diamond A + \Diamond B \\ | |||
\Diamond (A \cap B) & = & \Diamond A \cap \Diamond B \\ | |||
\Diamond (A \cup B) & = & \Diamond A \cup \Diamond B \\ | |||
\overline{\Diamond (\overline{A} + \overline{B})} & = & \Box A . \Box B \\ | |||
\overline{\Diamond (\overline{A} . \overline{B})} & = & \Box A + \Box B \\ | |||
\end{array} | |||
</math></div> | |||
''Proof of the first statement:'' | |||
<div align="center"><math> | |||
\begin{array}{r l} & \\ | |||
& \Box (A \cap B) \ = \\ | |||
= & \Box \lbrace \langle x, \min(\mu_A(x), \mu_B(x)), \max(\nu_A(x), \nu_B(x)) \rangle \ | \ x \in E \rbrace \\ | |||
= & \lbrace \langle x, \min(\mu_A(x), \mu_B(x)), 1 - \min(\mu_A(x), \mu_B(x)) \rangle \ | \ x \in E \rbrace \\ | |||
= & \lbrace \langle x, \min(\mu_A(x), \mu_B(x)), \max(1 - \mu_A(x), 1 - \mu_B(x)) \rangle \ | \ x \in E \rbrace \\ | |||
= & \lbrace \langle x, \mu_A(x), 1 - \mu_A(x) \rangle \ | \ x \in E \rbrace \cap \lbrace \langle x, \mu_B(x), 1 - \mu_B(x) \rangle \ | \ x \in E \rbrace \\ | |||
= & \Box A \cap \Box B | |||
\end{array} | |||
</math></div> | |||
== References == | |||
<references /> | |||
[[Category:Intuitionistic fuzzy sets]] | |||
Latest revision as of 18:14, 11 May 2017
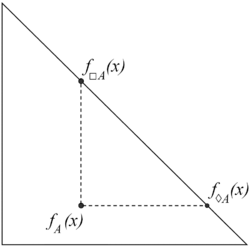
Necessity and possibility in the context of intuitionistic fuzzy sets are two modal operators defined as follows:
Let [math]\displaystyle{ E }[/math] be a fixed universe and [math]\displaystyle{ A \subset E }[/math] be a given set. Let functions [math]\displaystyle{ \mu_A, \nu_A \ : \ E \ \rightarrow [0,1] }[/math] determine the degrees of membership and non-membership. Then, the sets
[math]\displaystyle{ \Box A = \lbrace \langle x, \mu_A(x), 1 - \mu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]
[math]\displaystyle{ \Diamond A = \lbrace \langle x, 1 - \nu_A(x), \nu_A(x) \rbrace \ | \ x \in E \rbrace }[/math]
are called, respectively, necessity and possibility operators.
When [math]\displaystyle{ A }[/math] is a proper IFS, i.e. there exists an element [math]\displaystyle{ x \in E }[/math] for which [math]\displaystyle{ \mu_A(x) \gt 0 }[/math], then
[math]\displaystyle{ \Box A \subset A \subset \Diamond A }[/math]
[math]\displaystyle{ \Box A \ne A \ne \Diamond A }[/math].
Obviously, for every fuzzy set, i.e. intuitionistic fuzzy set with [math]\displaystyle{ (\forall x \in E)(\pi_A(x) = 0) }[/math] it holds that
[math]\displaystyle{ \Box A = A = \Diamond A }[/math].
These operators are meaningless in the case of fuzzy sets, hence, this is a demonstration that intuitionistic fuzzy sets are proper extensions of the ordinary fuzzy sets. Both operators were defined in May 1983 by Krassimir Atanassov.
Propositions about necessity and possibility
For every intuitionistic fuzzy set the following statements are valid:[1]
Proof of the first statement:
The following statements are also valid:[2]
Proof of the first statement:
References
- ↑ Proposition 1.42, page 61 from Intuitionistic Fuzzy Sets: Theory and Applications, Krassimir Atanassov, Springer, 1999.
- ↑ Theorem 1.43, page 62 from Intuitionistic Fuzzy Sets: Theory and Applications, Krassimir Atanassov, Springer, 1999.