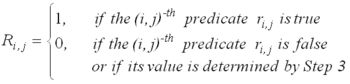Algorithm for transition functioning

The algorithm for generalized net transition functioning represents the algorithm of tokens transfer from an input place of a generalized net transition to its output place.

The algorithm comprises a "building block" for the entire algorithm for generalized net functioning, since the whole GN comprises of a set of sequentially connected transitions.

The first book where the algorithm was published, was the book "Generalized Nets" from 1991 year . The algorithm was modified in 2007 year .

When both algorithms are compared for a given transition, its functioning and the results of the work are equal, yet the difference is that in almost any case the new modified algorithm yields results more quickly than the original one.

Original algorithm, 1991

Step A01	Sort the input and output places of the transitions by their priorities. An important addition to the GN transition description above, which is related to the software implementation of the transition's functioning, is the following. The tokens from a given input place are divided into two groups. The first group contains those tokens that can be transferred to the transition output, while the second group contains the rest tokens. Let both groups be denoted by [math]\displaystyle{ P_1(l) }[/math] and [math]\displaystyle{ P_2(l) }[/math], respectively, where [math]\displaystyle{ l }[/math] is the corresponding place.
Step A02	Sort the tokens from group [math]\displaystyle{ P_1(l) }[/math] of the input places (following the order from Step A01) by their priorities. Let ri,j denote the predicate index matrix of the transition. Then, let us make the following assumption:
Step A03	Assign value 0 to all elements of R, for which either the input place which corresponds to the respective predicate is empty (the [math]\displaystyle{ P_1(l) }[/math] part is empty); or the output place which corresponds to the respective predicate is full; or the current capacity of the arc between the corresponding input and output places is 0.
Step A04	Calculate the values of the other elements of matrix r and assign the obtained values to the elements of matrix R.
Step A05	Calculate the values of the characteristic functions related to the corresponding output places in which tokens will enter. Assign these characteristics to the entering tokens.
Step A06	Perform the following sub-steps for each input place by the order of input place priorities: Select the tokens with the highest priority in this input place; Transfer the selected tokens to all output places, for which the corresponding predicate enables this (the tokens go to group [math]\displaystyle{ P_2(l) }[/math] of the output places).
Step A07	Transfer the tokens with the highest priority, for which all calculated values of the predicates are equal to "false" to the group [math]\displaystyle{ P_2(l) }[/math] of the corresponding places. To this group, also transfer all tokens that cannot be transferred to the corresponding output places because these places have already been filled up with tokens from other places with higher priorities.
Step A08	Add t0 to the current time, i.e., TIME := TIME + t0
Step A09	Check whether the value of the current time is less than t1 + t2 (the time- components of the considered transition).
Step A10	If the answer to the question on Step A09 is "yes", go to Step A02 (to update the tokens' order in the places).
Step A11	If the answer to the question on Step A09 is "no", terminate the current functioning of the transition.

Modified algorithm, 2007

Step A*01	The input and the output places are arranged by priority.
Step A*02	In each input place two lists are formed: a list of all tokens, arranged by priority, and an empty list.
Step A*03	An empty index matrix R, which corresponds to the matrix of the predicates r of the given transition, is generated. It is initialized with a value "0" (corresponding to value "false") of all of the elements of this new matrix, which: are placed in a row, corresponding to an empty input place, are placed in a column, corresponding to a full output place, are placed in (i,j)-th position, for which mi,j = 0, i.e. the current capacity of the arc between i-th input and j-th output place is zero.
Step A*04	The sorted places are passed sequentially by their priority, starting with the place having the highest priority, which has at least one token and through which no transfer has occurred on the current time-step. For its highest priority token (from the first list) the predicates corresponding to the relevant row of matrix R are checked. The elements of r, for which the elements of R are not zeros, are calculated.
Step A*05	Depending on the execution of the operator for permission or prohibition of tokens splitting over the net, the token from Step A*04 will pass either to all permitted to it output places, or to this very place among them, which has the highest priority. If one token cannot pass through a given transition on this time interval, it is moved to the second list of tokens of the corresponding place. The tokens, which have entered the place after the transition activation, are moved to the second list, too.
Step A*06	The capacities of all places on the output of the transition, which are input places for another currently active transitions, increment with 1 for each token that has left them on this step.
Step A*07	The capacities of all output places, in which a token, determined at Step A*04, has entered, decrement with 1. If the maximum number of tokens for a given output place has been reached, the elements of the corresponding column of matrix R are set to value "0".
Step A*08	The capacities of all arcs, through which a token has passed, decrement with 1. If the capacity of an arc has reached 0, the elements of the corresponding output place of matrix R are set to value 0.
Step A*09	The values of the characteristic function Φ for the output places, in which tokens have entered (formed by the token passed according to Step A*05) are calculated.
Step A*10	If there are more places, which could be output ones for tokens at this step, the algorithm returns back to Step A*04; in the opposite case it proceeds to Step A*11.
Step A*11	The current model time t is increased with t0.
Step A*12	Is the current time moment equal to or greater than t1 + t2? If the answer of the question is "no", return to Step A*04. Otherwise, the transition functioning terminates.