Transition

A GN transition with m inputs and n outputs

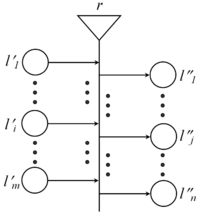
Transition in the context of generalized nets is an object from the static structure of the net, which comprises the conditions of tokens' transfer from the transition's input places to its output places.

When tokens enter the input place of a transition, it becomes potentially fireable and at the moment of their transfer towards the transition's output places, the transition is being fired.

The tokens' transfer through a transition is described by a special formal algorithm.

Formal description

Formally, every transition is described by a 7-tuple:

[math]\displaystyle{ Z = \langle L', L'', t_1, t_2, r, M, \Box \rangle }[/math]

where:

• [math]\displaystyle{ L', L'' }[/math] are finite, non-empty sets of places: the transition's input and output places, respectively.
• [math]\displaystyle{ t_1 }[/math] is the current time-moment of the transition's firing.
• [math]\displaystyle{ t_2 }[/math] is the current value of the duration of its active state.
• [math]\displaystyle{ r }[/math] is the transition's condition, determining which tokens will transfer from the transition's inputs to its outputs. The parameter has the form of an index matrix:

  [math]\displaystyle{ r = \begin{array}{c|c c c c c} & l''_1 & ... & l''_j & ... & l''_n \\ \hline l'_1 & & & & & \\ ... & & & & & \\ l'_i & & & r_{i,j} & & \\ ... & & & & & \\ l'_m & & & & & \\ \end{array} }[/math]

  where [math]\displaystyle{ r_{i,j} }[/math] are predicates, [math]\displaystyle{ 1 \le i \le m, 1 \le j \le n }[/math]

• [math]\displaystyle{ M }[/math] is the index matrix of the capacities of the transition's arcs:

  [math]\displaystyle{ M = \begin{array}{c|c c c c c} & l''_1 & ... & l''_j & ... & l''_n \\ \hline l'_1 & & & & & \\ ... & & & & & \\ l'_i & & & M_{i,j} & & \\ ... & & & & & \\ l'_m & & & & & \\ \end{array} }[/math]

  where [math]\displaystyle{ M_{i,j} \ge 0 }[/math] are natural numbers or [math]\displaystyle{ \infty }[/math], [math]\displaystyle{ 1 \le i \le m, 1 \le j \le n }[/math]

• [math]\displaystyle{ \Box }[/math] is called transition's type, an object having a form similar to a Boolean expression. It may contain as variables the symbols that serve as labels for transition's input places, and it is an expression constructed of variables and the Boolean connectives [math]\displaystyle{ \land }[/math] and [math]\displaystyle{ \lor }[/math] determining the following conditions:

  [math]\displaystyle{ \land(l_{i_1}, l_{i_2},...,l_{i_u}) }[/math] - each of the places [math]\displaystyle{ l_{i_1}, l_{i_2},...,l_{i_u} }[/math] must contain at least one token,

  [math]\displaystyle{ \lor(l_{i_1}, l_{i_2},...,l_{i_u}) }[/math] - there must be at least one token in the set of places [math]\displaystyle{ l_{i_1}, l_{i_2},...,l_{i_u} }[/math] where [math]\displaystyle{ \lbrace l_{i_1}, l_{i_2},...,l_{i_u} \rbrace \subset L' }[/math]

  When the value of a type (calculated as a Boolean expression) is "true", the transition can become active, otherwise it cannot.

References

• On Generalized Nets Theory, Krassimir Atanassov, Prof. Marin Drinov Academic Publishing House, Sofia, 2007