Place

Figure 1.

Figure 2.

Places in the generalized nets are the second basic component of its static structure together with the transitions.

Types of GN places

A place can play two roles with respect to a given transition:

• input place for the transition,
• output place for the transition.

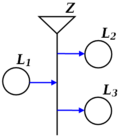
Example: On Figure 1, place [math]\displaystyle{ L_1 }[/math] is input for transition [math]\displaystyle{ Z }[/math] and places [math]\displaystyle{ L_2, L_3 }[/math] are outputs for this transition.

A place that does not serve as a general input or output place for the whole generalized net, serves both as an output place for one transition and as an input place for another.

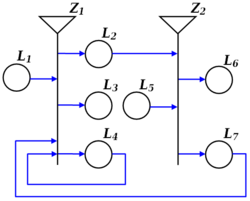
Example: On Figure 2, the net's general inputs are places [math]\displaystyle{ L_1 }[/math] and [math]\displaystyle{ L_5 }[/math] and its general outputs are places [math]\displaystyle{ L_3 }[/math] and [math]\displaystyle{ L_6 }[/math]. Place [math]\displaystyle{ L_2 }[/math] is output for transition [math]\displaystyle{ Z_1 }[/math] and is input for transition [math]\displaystyle{ Z_2 }[/math].

Some places are both input and output places for one transition; i.e. the tokens there can do loop.

Example: On Figure 2, such places are [math]\displaystyle{ L_4 }[/math] and [math]\displaystyle{ L_7 }[/math].

Places and index matrices

The sets of input and output places of a given transition take part in the construction of its index matrix of predicates. The rows of the index matrix are labeled with the labels of the input places. The columns of the index matrix are labeled with the labels of the output places. The matrix element [math]\displaystyle{ {IP_i, OP_j} }[/math] that stays on the intersection of the [math]\displaystyle{ i }[/math]-th matrix row and [math]\displaystyle{ j }[/math]-th matrix column practically corresponds to the predicate that determines whether a token can pass from the [math]\displaystyle{ i }[/math]-th input place and [math]\displaystyle{ j }[/math]-th output place of the transition. When constructing the index matrix of a transition, it is important to take into consideration the eventual loops.

Example: Figure 3 represents the index matrix of transition [math]\displaystyle{ Z_1 }[/math] from the simple generalized net, given on Figure 2. It is noteworthy that places [math]\displaystyle{ L_4 }[/math] and [math]\displaystyle{ L_7 }[/math] are input places for the transition [math]\displaystyle{ Z_1 }[/math]. For the needs of the example, the values of the predicates have been randomly chosen; they do not follow from the graphical structure of the model, but rather from the logic of the modelled process.

IM =	L2 L3 L4 L1 false false true L4 W4,2 false W4,4 L7 W7,2 W7,3 false

Figure 3.