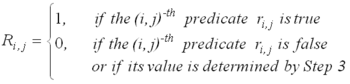Algorithm for transition functioning

The algorithm for generalized net transition functioning represents the algorithm of GN tokens transfer from an input place of a GN transition to its output place.

The algorithm comprises a "building block" for the entire algorithm for generalized net functioning.

The first book it was published in, was the book "Generalized Nets" from 1991 year . The algorithm was later modified in 2007 .

The functioning and the results of the work of a given GN transition are equal for both the original and the modified algorithms, yet the difference between both is that in almost any case the modified algorithm yields results more quickly.

Original algorithm, 1991

Step 1	Sort the input and output places of the transitions by their priorities. An important addition to the GN transition description above, which is related to the software implementation of the transition's functioning, is the following. The tokens from a given input place are divided into two groups. The first group contains those tokens that can be transferred to the transition output, while the second group contains the rest tokens. Let both groups be denoted by P1(l) and P2(l), respectively, where l is the corresponding place.
Step 2	Sort the tokens from group P1 of the input places (following the order from Step 1) by their priorities. Let ri,j denote the predicate index matrix of the transition. Then, let us make the following assumption:
Step 3	Assign value 0 to all elements of R, for which either the input place which corresponds to the respective predicate is empty (the P1 part is empty); or the output place which corresponds to the respective predicate is full; or the current capacity of the arc between the corresponding input and output places is 0.
Step 4	Calculate the values of the other elements of matrix r and assign the obtained values to the elements of matrix R.
Step 5	Calculate the values of the characteristic functions related to the corresponding output places in which tokens will enter. Assign these characteristics to the entering tokens.
Step 6	Perform the following sub-steps for each input place by the order of input place priorities: Select the tokens with the highest priority in this input place; Transfer the selected tokens to all output places, for which the corresponding predicate enables this (the tokens go to group P2 of the output places).
Step 7	Transfer the tokens with the highest priority, for which all calculated values of the predicates are equal to "false" to the group P2 of the corresponding places. To this group, also transfer all tokens that cannot be transferred to the corresponding output places because these places have already been filled up with tokens from other places with higher priorities.
Step 8	Add t0 to the current time, i.e., TIME := TIME + t0
Step 9	Check whether the value of the current time is less than t1 + t2 (the time- components of the considered transition).
Step 10	If the answer to the question on Step 9 is "yes", go to Step 2 (to update the tokens' order in the places).
Step 11	If the answer to the question on Step 9 is "no", terminate the current functioning of the transition.